ML: Тензоры в Keras

Введение

Нейронная сеть - это функция $\mathbf{T}' = F(\mathbf{T})$, которая преобразует один тензор $\mathbf{T}$ в другой $\mathbf{T'}$.

Существует несколько фреймворков (tensorflow, pytourch), которые обеспечивают эффективное вычисление подобных функций, в том числе на GPU. Первоначально синтаксис таких фреймворков был достаточно громоздким, поэтому Франсуа Шолле написал библиотеку в виде библиотеки keras, которая существенно упростила проектирование нейронных сетей. Со временем keras была поглощена Google и теперь развивается только в составе tensorflow версии 2.0 и выше.

На самом деле, фреймворки не только вычисляют функцию $F(\mathbf{T})$ (прямое распространение), но и решают сложную задачу оптимизации, подбирая параметры функции (обратное распространение ошибки). Тем не менее в этом документе мы сосредоточимся на первой задаче. Понимание того, как происходит вычисление $F(\mathbf{T})$ на каждом этапе, необходимо для понимания работы сложных архитектур нейронных сетей.

Используемые ниже слои будем импортировать из tensorflow: 

  
from tensorflow.keras.layers  import Input,   Dense, SimpleRNN, Lambda
from tensorflow.keras.layers  import Flatten, Dot,   Activation

Тензоры в backend

Библиотека keras на нижнем уровне раньше могла работать с тензорами numpy, tensorflow или theano. Поэтому по традиции она оборачивает тензоры в свой собственный класс. Для этого используется окружение backend: 

  
import tensorflow.keras.backend as K

Так как тензоры участвуют в алгоритмах оптимизации, возникает необходимость различать постоянные (constant) и переменные (variable) тензоры: 

          
cnst = K.constant(value = np.array([ [1, 2], [3, 4]]),  # numpy массив
                  dtype = 'float32',                    # тип его элементов
                  name  = 'my_cnst')                    # имя (для ссылок)

print( type ( cnst  ) )     #>  tensorflow.python.framework.ops.EagerTensor
print( cnst )               #>  tf.Tensor( [[1. 2.] [3. 4.]], shape=(2, 2), dtype=float32)

Так как keras (вне tensorflow) может работать с различными бэкэндами, возвращаемый методом объект может быть, как numpy тензором, так и тензором tensorflow. Поэтому к их свойствам стоит "достукиваться" через функции backend: 

          
print( K.dtype(cnst) )      #>  float32
print( K.int_shape(cnst) )  #>  (2, 2)

Аналогично для переменных: 

          
var = K.variable(value = np.array([ [1, 2], [3, 4]]),  # numpy массив
                 dtype = 'float64',                    # тип его элементов                
                 name  = 'my_var')                     # имя (для ссылок)

print( type ( var  ) )    #>  tensorflow.python.ops.resource_variable_ops.ResourceVariable
print( var )              #>  tf.Variable 'my_var:0' shape=(2, 2) dtype=float64, 
                          #>  numpy= array([[1., 2.], [3., 4.]])

С тензорами keras можно обращаться подобно numpy тензорам: 

  
t = K.ones((2, 3))                   # матрица 2x3 из единиц

t1 = t[:, 0]                         # первая колонка
t2 = t[:, 1]                         # вторая колонка
t3 = K.concatenate([t1, t2])         # их объединение в один вектор

print(t1)                            #> tf.Tensor([1. 1.], shape=(2,), dtype=float32)
print(K.eval(t1))                    #> [1. 1.]
print(K.eval(t3))                    #> [1. 1. 1. 1.]

type(t1)                             #> tensorflow.python.framework.ops.EagerTensor

Объекты слоёв

Нейронные сети состоят из соединённых между собой слоёв. Слои являются "элементарными" функциями из которых формируется финальная модель $F(\mathbf{T})$. Каждый слой является классом. Экземпляр этого класса получает на вход тензор и выдаёт на выход тензор, вообще говоря, другой размерности и формы. У слоёв keras есть две ключевые особенности:

  • При обработке тензора не затрагивается его нулевая ось.
  • Объявление слоя ещё не приводит к вычислению.

Первая особенность связана с тем, что вычисления выполняются не для одного тензора, а для их набора (батча) размера batch_size. В задачах машинного обучения каждый тензор батча это один пример. При оптимизации параметров модели, ошибка вычисляется по всем примерам батча.

По факту любой слой Layer является элементарной функцией, которая производит вычисления независимо для каждого примера (хотя часто делает это "одновременно" и очень эффективно для всех примеров сразу): 

  
   for i in range(x.shape[0]):
      y[i] = Layer(x[i])
(в numpy запись x[i] для тензора, например, размерности три, означает x[i,:,:] - i-я матрица пачки).

Вторая особенность связана с тем, что все преобразования с тензорами формируют вычислительный граф. Прямой проход по этому графу приводит к вычислению тензоров (и выхода нейронной сети), а обратный - к вычислению градиентов, необходимых при оптимизации параметров модели.

Слой Activation

Рассмотрим слой Activation, который вычисляет заданную функцию от каждого элемента тензора. Параметров для обучения у слоя нет и форма тензора на выходе совпадает с формой на входе.

Вычислим в numpy, например, гиперболический тангенса от тензора с формы (2,3): 

  
val = np.array([ [1, 0, -1],   # val.shape = (2,3)
                 [2, 0, -2]])
y = np.tanh(val)

В библиотеке keras мы должны преобразовать входной numpy-тензор val в keras-тензор x. Затем создаём экземпляр "a" класса слоя Activation и ему передаём входной тензор x. Слой возвращает выходной тензор y: 

  
x =  K.variable( val )         # тензор keras из numpy тензора val
                              
a = Activation('tanh')         # экземпляр объекта Activation
y = a(x)                       # y - тензор после обработки тензора x

print( y )                     # Tensor("activation_10/Tanh:0", shape=(2,3), dtype=float32)

print( K.eval(y) )             # [[ 0.762  0.    -0.762]
                               #  [ 0.964  0.    -0.964]]
Обратим внимание, что числа (собственно вычисления) получаются только после вызова K.eval(y). Эта функция запускает работу вычислительного графа ведущего в узел y.

Создание слоя и получение выходного тензора можно объединить в одной строчке. Например вычислим функцию softmax: 

 
y = Activation('softmax')(x)  

print(K.eval(y))               # [[0.665 0.245 0.09 ]
                               #  [0.867 0.117 0.016]]
Эта функция $e^{x_{i \alpha}}/\sum_\beta e^{x_{i\beta}}$ задействует не только данный элемент $x_{i\alpha}$, но и (для нормировки) все остальные элементы по первой оси (второй индекс). В результате сумма чисел по каждому примеру батча оказывается равной 1 (что, обычно, используется в финальном слое для получения "вероятностей" классов).

Слой Flatten

Слой Flatten также не имеет параметров для обучения, но меняет форму тензора. Задача этого слоя состоит в преобразовании многомерного входного тензора в одномерный тензор (без учёта оси батча!).
На numpy это может выглядеть так: 

  
x = np.arange(12)                  
x.shape = (2,2,3)              #  вход - стопка из двух матриц 2x3

y = x.reshape(x.shape[0], -1)  #  выход - "стопка" из векторов

print(y)                       #  [[ 0  1  2  3  4  5]
                               #   [ 6  7  8  9 10 11]]

На keras эти же вычисления выглядят следующим образом: 

  
x = K.arange(12)               # тензор keras [0,...,11]
x = K.reshape(x, (2,2,3))      # меняем его форму
                              
f = Flatten()                  # экземпляр объекта Flatten
y = f(x)                       # y - тензор после обработки тензора x

print( x.shape )               #> (2, 2, 3)
print( y.shape )               #> (2, 6)

print( K.eval(y) )             #> [[ 0  1  2  3  4  5]      <- обычный numpy массив
                               #   [ 6  7  8  9 10 11] ]

Таким образом, слой Flatten следующим образом меняет размерность тензора: 
  
(batch_size, d1,d2,...,dn)   =>  (batch_size, d1*d2*...*dn)

Полносвязный слой Dense

Слой Dense состоит из units нейронов, соединённых синапсами с элементами входного тензора по его последнему индексу. Пусть размерность этого индекса равна inputs = x.shape[-1]. Обучаемыми параметрами слоя Dense является матрица $\mathbf{W}$ формы (inputs, units) и вектор $\mathbf{b}$ формы (units, ). Слой выполняет линейное преобразование:

$$ y_{...j} = \sum^{\mathrm{inputs}-1}_{i=0} x_{...i}\, W_{ij} + b_j, $$

где многоточие обозначает, вообще говоря, произвольное число индексов, по-мимо обязательного нулевого индекса примеров батча: (batch_size,...,inputs) (inputs, units) + (units, ).

Ниже, в качестве матрицы $\mathbf{W}$, задаётся матрица, состоящая из единиц (если этого не сделать, её элементы будут случайными). При помощи параметра use_bias указывается, что вектор $\mathbf{b}$ нам не нужен: 

 
x = K.reshape(K.arange(6, dtype="float32"), (2,3))   

W = np.ones((3,4))

d = Dense(units=4, weights = [W], use_bias = False)
y = d(x)

K.eval(y)         # вычисление произведения

В табличной форме входная матрица $\mathbf{x}$ состоит из двух строк (batch_size=2) и трёх колонок (три признака у каждого из двух примеров). Так как число нейронов равно units=4, матрица весов имеет форму (3, 4):

$$ \mathbf{x}\cdot \mathbf{W} ~=~ _\text{batch_size} \Bigg\{ \overbrace{ \begin{array}{|c|c|c|} \hline 0 & 1 & 2 \\ \hline 3 & 4 & 5 \\ \hline \end{array} }^{\mathrm{inputs}} ~~~\cdot~~~ _\text{inputs} \Bigg\{ \overbrace{ \begin{array}{|c|c|c|c|} \hline 1 & 1 & 1 & 1 \\ \hline 1 & 1 & 1 & 1\\ \hline 1 & 1 & 1 & 1\\ \hline \end{array} }^{\mathrm{units}} ~ = ~ _\text{batch_size} \Bigg\{ \overbrace{ \begin{array}{|c|c|c|c|} \hline 3 & 3 & 3 & 3 \\ \hline 12 & 12 & 12 & 12 \\ \hline \end{array} }^{\mathrm{units}} ~ = ~ \mathbf{y}. $$

При добавлении вектора смещения (bias) к матрице используется правило расширения (broadcasting). По этому правилу вектор превращается в матрицу (inputs, units) с одинаковыми строчками.

Подчеркнём, что размерность входного тензора может быть любой: 

 
x = K.ones((2,3,4,5))
y = Dense(8)(x)

print(y.shape)             # (2, 3, 4, 8)

Матрица в объекте слоя Dense создаётся, когда к нему присоединяется входой тензор (и становится известным размерность его последнего индекса: 

 
d = Dense(1)
print( d.weights )   #> []

x = K.ones((2,3))     
y = d(x)

print(d.weights)     #> [[-1.132], [ 0.808],  [-0.135]]

Таким образом, слой Dense с units нейронами и размерностью inputs последнего индекса входного тензора, имеет (inputs+1)*units параметров, если есть смещение $\mathbf{b}$ и inputs*units, если его нет. Форму тензора слой менят следующим образом: 
  
(batch_size, d1,d2,...,dn, inputs)   =>  (batch_size, d1,d2,...,dn, units)

Свёрточный слой Conv2D

Свёрточный слой Conv2D применяется к "картинкам" высотой rows, шириной cols и имеющих channels "цветовых" каналов. На самом деле графические термины условны и слой Conv2D может применяться не только при обработке изображений. Важно, что входящий в него тензор должен иметь форму: 

 
x.shape = (batch_size, channels, rows, cols) если data_format = "channels_first"
x.shape = (batch_size, rows, cols, channels) если data_format = "channels_last" (по умолч.)
Для определённости будем использовать второй порядок, принятый в keras по умолчанию.

Задача слоя Conv2D состоит в обработке "изображения" небольшим фильтром, который по нему скользит. Фильтрация проводится одновременно по всем каналам. Ниже на рисунке картинка (вход x) имеет 3 строки, 4 колонки и 2 канала. Размер ядрa фильтра 2x2 пикселя и 2 в глубину для каналов (3D тензор: голубой кубик).

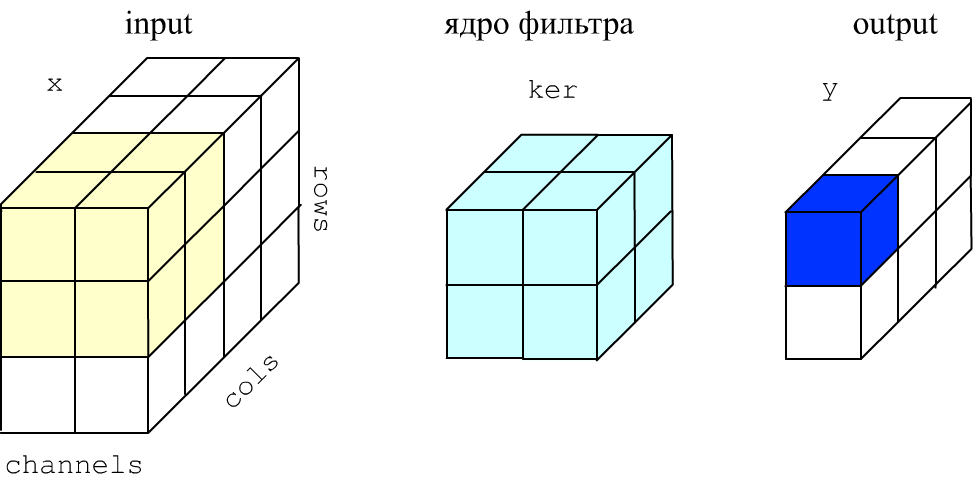
Элементы ядра (определяющие фильтр) перемножаются с соответствующими элементами такого же кубика на картинке (жёлтый цвет). Эти произведения складываются и к ним добавляется смещение bias (ещё один параметр фильтра). Результат вычислений помещается в первый пиксель на выходе y слоя (синий цвет). Затем жёлтый "кубик" сдвигается вправо (по умолчанию на один пиксель) и вычисляется следующее значение выхода.

У слоя может быть не один, а несколько фильтров с различными ядрами и смещениями (ниже голубой и салатовый кубики). В этом случае описанные выше вычисления проделываются для каждого фильтра f независимо. Выход слоя будет иметь число каналов (глубину) равное числу фильтров:

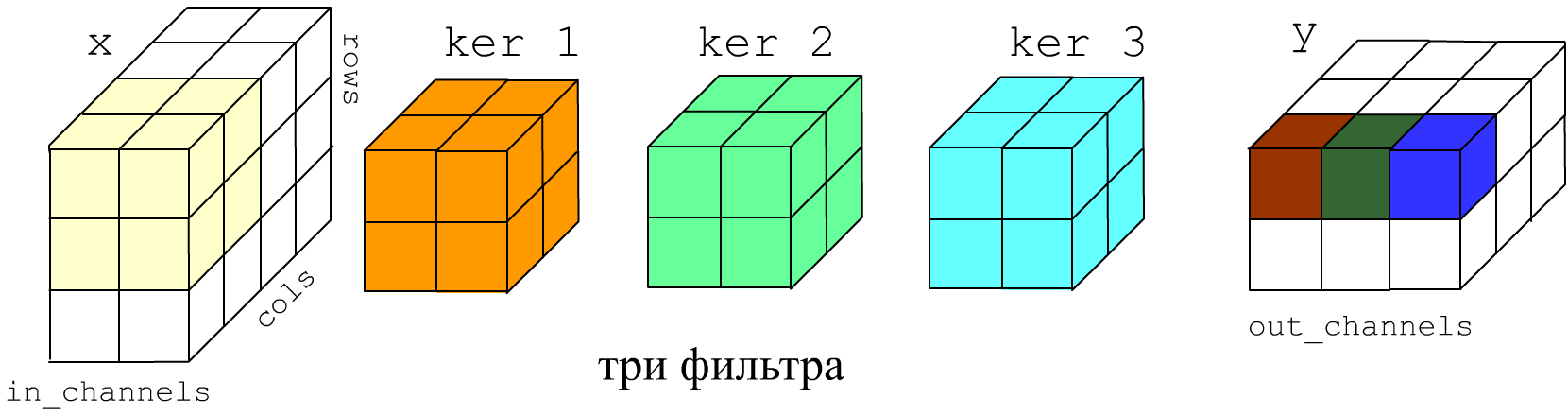
У слоя Conv2D есть два обязательных параметра:

Слой создаёт 4D тензор ядра фильтра ker формы (k_rows, k_cols, channels, filters) и вектор формы ( filters, ) для смещений bias каждого фильтра. Вычисления для "пикселя" c координатами (r,c) выглядят следующим образом: 
 

y[s, r, c, f] = np.sum( x[s, r:r+h, r:c+w, :] * ker[:, :, :, f] ) + bias[f].

Свёртка на numpy и keras

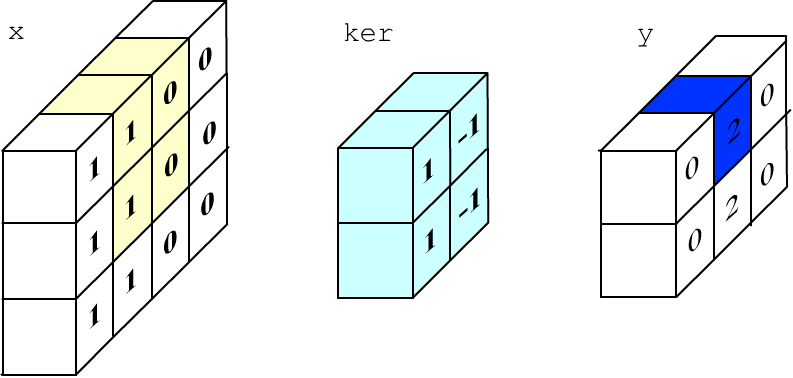
Рассмотрим пример вычисления свёртки при помощи numpy. Пусть картинка имеет 3 строки, 4 колонки и содержит один канал. Заполним левую её половину единицами ("белый цвет"), а правую - нулями ("чёрный цвет"): 

 
channels, filters = 1, 1                          # один канал, один фильтр
x_rows, x_cols    = 3, 4                          # размер картинки на входе

im = np.ones((x_rows, x_cols), dtype = 'float32') # левая половина картинки "белая"
im[:, 2:] = 0                                     # а правая половина - "чёрная"
Обработаем картинку свёрточным слоем с одним фильтром и ядром размера 2x2 (ниже это будет фильтр выделения вертикального края). Будем считать, что у фильтра смещения нет: 
 
k_rows, k_cols    = 2, 2                          # размер ядра

y_rows = x_rows-k_rows+1                          # размер картинки на выходе
y_cols = x_cols-k_cols+1                          # (фильтр смещается на один пиксель)

x = im.reshape( (1, x_rows, x_cols, channels) )   # вход
y = np.empty  ( (1, y_rows, y_cols, filters ) )   # выход

ker = np.array( [ 1,-1,  1,-1   ] )               # ядро фильтра                  
ker.shape = (k_rows, k_cols, channels, filters)   # выделения вертикального края

for r in range(y_rows):                           # проведение свёртки
    for c in range(y_cols):
        y[0,r,c,0] = np.sum( x[0, r:r+k_rows, c:c+k_cols, :] * ker[ :, :, :, 0] )

Процесс вычисления одного пикселя выхода приведен на рисунке ниже (1*1+0*(-1)+1*1+0*(-1)=2):

Теперь выполним эти же вычисления на keras: 

 
x = K.variable(value = im.reshape( (1, x_rows, x_cols, channels) ))

con = Conv2D(filters = 1, kernel_size = (k_rows, k_cols), 
             use_bias = False, weights = [ker] )

print(x.shape,"=>", y.shape)                     #> (1, 3, 4, 1) => (1, 2, 3, 1) 
print(K.eval(y).reshape(-1))                     #> [0, 2, 0, 
                                                 #   0, 2, 0]

Таким образом, слой Conv2D с filters фильтрами и формой каждого фильтра kernel_size=(k_rows, k_cols) имеет filters*(k_rows*k_cols + 1) параметров (если есть смещение). Форму тензора слой меняет следующим образом: 
  
(batch_size, x_rows, x_cols, channels)  =>  (batch_size, y_rows, y_cols, filters)

Значения (y_rows, y_cols) зависят от (x_rows, x_cols), размеров ядра фильтра (k_rows, k_cols) и того как фильтр скользит по входной картинке. Это движение определяется параметрами:

Универсальный слой Lambda

Если слои со стандартным поведением не подходят, можно воспользоваться слоем Lambda. Этому слою передаётся произвольная lambda-функция меняющая входящий в слой тензор. Единственное ограничение: внутри lambda-функции можно использовать только функции по работе с тензорами из backend. В противном случае keras не сможет вычислить градиент при обратном распространении ошибки.

Вычислим, например,сумму компонент входного тензора по axis=1 (второй индекс "признаков"): 

  
x = K.variable(value = np.array([[1,2,3],  [4,5,6]]) )

lm = Lambda(lambda t: K.sum(t,axis=1))
y  = lm(x)

print( K.eval(y) )                    #>  [ 6. 15.]

На слой можно передать несколько тензоров, при помощи их списка. В качестве простого примера, сложим два тензора внутри lambda-функции: 

  
x1 = K.variable(value = np.array([[1,2,3],  [4,5,6]]) )
x2 = K.variable(value = np.array([[7,8,9],  [1,2,3]]) )

lm = Lambda(lambda lst: lst[0]+lst[1])
y  = lm([x1,x2])

print( K.eval(y) )                    #> [[ 8. 10. 12.]
                                      #   [ 5.  7.  9.]]