ML: Логика и вероятность. Часть II
Введение
Формальная логика является частным случаем теории вероятностей. Этот документ является непосредственным продолжением введения в логику и формальные теории. Теперь мы обсудим каким образом, при помощи теории вероятностей, можно обобщить бинарную логику на случай вероятностных моделей.
Вывод в теории вероятностей
Ограничимся сначала логическими теориями, сигнатура которых содержит только высказывания. Будем их интерпретировать как события. Подчеркнём, что в отличии от многозначной или нечёткой логик, в рассматриваемой здесь вероятностной логике справедлив закон исключения третьего. Это означает, что любое высказывание считается или истинным или ложным (событие или произойдёт, или не произойдёт). Однако иногда мы способны указать только вероятность того или иного значения.
Заглавными буквами в теории вероятности удобно обозначать событие $A$, а прописными $\{a,\bar{a}\}$ - его "значение" (произошло, не произошло). Такое соглашение позволяет единообразно рассматривать события и случайные величины, принимающих более двух значений. Следует отличать обозначения в которых $P(A)$ - вероятность того, что событие произошло, а $P(\bar{A})=1-P(A)$ - что не произошло, от соглашений в которых $P(A)$ - этот вектор с компонентами $\{P(a),P(\bar{a})\}$, а условная $P(A\to B)$ или совместная $P(A,B)$ вероятности - это матрицы 2x2. Теперь запись $P(\bar{A})=1-P(A)$ означает две формулы $P(\bar{a})=1-P(a)$ и $P(a)=1-P(\bar{a})$, так как для событий считаем, что $\bar{\bar{a}}=a$.
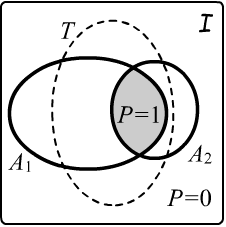 Наделим множество интерпретаций "метрикой", присвоив каждой интерпретации
некоторую вероятность.
Вероятность любой формулы равна сумме вероятностей интерпретаций из области её истинности.
Кроме этого, будем считать, что суммарная вероятность интерпретаций,
удовлетворяющих данной формальной теории (все её модели) равна единице. Соответственно,
вероятности остальных интерпретаций в этой теории равны нулю.
Наделим множество интерпретаций "метрикой", присвоив каждой интерпретации
некоторую вероятность.
Вероятность любой формулы равна сумме вероятностей интерпретаций из области её истинности.
Кроме этого, будем считать, что суммарная вероятность интерпретаций,
удовлетворяющих данной формальной теории (все её модели) равна единице. Соответственно,
вероятности остальных интерпретаций в этой теории равны нулю.
Справа на рисунке закрашенная область (пересечение областей истинности аксиом $A_1,A_2$) содержит интерпретации, сумма вероятностей которых равна единице. Интерпретации в незакрашенных областях имеют нулевые вероятности. В результате, каждая аксиома и выводимая в логике из них теорема имеет единичную вероятность: $P(A_1)=P(A_2)=P(T)=1$. Поэтому, чтобы выяснить, является ли утверждение истинным в данной теории, необходимо найти его вероятность.
Правила вывода
Напомним, что вероятность события $B$ при условии, что произошло событие $A$, мы обозначаем на логический манер, как $P(A\to B)$, вместо общепринятого $P(B\,|\,A)$. Совместная вероятность наступления двух событий обозначается как $P(A\,\&\,B)$ или просто $P(A,\,B)$. Рассмотрим несколько примеров стандартных логических выводов в терминах теории вероятностей.
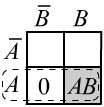 ✒ В логике импликацию $A\to B$ можно заменить на дизъюнкцию $\bar{A}\vee B$ и наоборот.
✒ В логике импликацию $A\to B$ можно заменить на дизъюнкцию $\bar{A}\vee B$ и наоборот.
В теории вероятностей
выполняется следующее равенство: $P(A)\,(1-P(A\to B)) = 1-P(\bar{A}\vee B)$.
Поэтому при любых $A=\{a,\bar{a}\}$ и $B=\{b,\bar{b}\}$ и $P(A)\gt 0$
справедлив двухсторонний вывод:
$$
P(A\to B) = 1 ~~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~~~P(\bar{A}\vee B) = 1.
$$
Напомним также, что, в силу определения условной вероятности, при этом $P(A,B)=P(A)$,
что сразу приводит к $P(A,\bar{B})=0$, см. рисунок справа.
Это означает, что оставшиеся клетки (интерпретации) в сумме имеют единичную вероятность,
а они равны $\bar{A}\vee B$, что есть объединение первой строки ($\bar{A}$) и второй колонки ($B$).
✒
 Аналогично правило обращения импликации:
$
A\to B~~\Rightarrow~~\bar{B}\to \bar{A}
$
на языке теории вероятностей имеет вид:
$$
P(A\to B) = 1~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~P(\bar{B}\to \bar{A}) = 1.
$$
Для доказательства можно воспользоваться предыдущим правилом или получить
$P(\bar{B}\to\bar{A})=1$ от противного, показав, что $P(\bar{B}\to A)=0$:
$$
P(\bar{B})\,P(\bar{B}\to A) = P(A,\bar{B}) = P(A)\,P(A \to \bar{B}) = 0,
$$
где $P(A \to \bar{B})=0$ по формуле полной вероятности из $P(A \to B)=1$.
Так как в логике и в теории вероятностей для событий $\bar{\bar{A}}=A$, $\bar{\bar{B}}=B$,
этот вывод можно считать двухсторонним. Ещё один способ доказательства - это
использования того факта, что при $P(A\to B)=1$ в пространстве испытаний
$A\subseteq B$, откуда очевидно, что $\bar{B}\subseteq \bar{A}$.
Аналогично правило обращения импликации:
$
A\to B~~\Rightarrow~~\bar{B}\to \bar{A}
$
на языке теории вероятностей имеет вид:
$$
P(A\to B) = 1~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~P(\bar{B}\to \bar{A}) = 1.
$$
Для доказательства можно воспользоваться предыдущим правилом или получить
$P(\bar{B}\to\bar{A})=1$ от противного, показав, что $P(\bar{B}\to A)=0$:
$$
P(\bar{B})\,P(\bar{B}\to A) = P(A,\bar{B}) = P(A)\,P(A \to \bar{B}) = 0,
$$
где $P(A \to \bar{B})=0$ по формуле полной вероятности из $P(A \to B)=1$.
Так как в логике и в теории вероятностей для событий $\bar{\bar{A}}=A$, $\bar{\bar{B}}=B$,
этот вывод можно считать двухсторонним. Ещё один способ доказательства - это
использования того факта, что при $P(A\to B)=1$ в пространстве испытаний
$A\subseteq B$, откуда очевидно, что $\bar{B}\subseteq \bar{A}$.
Благодаря этому правилу, если известно, что для конкретных значений
$P(a\to \bar{b})=1$, то и $P(\bar{a}\to b)=1$.
При этом, по формуле полной вероятности, оставшиеся значения равны нулю: $P(a\to b)=P(\bar{a}\to \bar{b})=0$.
Таким образом, единичная условная вероятность фиксирует условные вероятности для всех остальных значений.
 ✒ Ещё одно двухстороннее следствие $C\to A,~C\to B~~~~\Leftrightarrow~~~~C\to A\,\&\,B~~$ имеет вид:
$$
P(C\to A) = P(C\to B) = 1 ~~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~~~P(C \to A,B) = 1.
$$
Справа-налево оно доказывается при помощи формулы полной вероятности. Так как $P(C\to A,B)=1$, то
$$
P(A,B,C) = P(C)= P(A,B,C) + P(A,\bar{B},C) + P(\bar{A},B,C) + P(\bar{A},\bar{B},C).
$$
Так как все вероятности неотрицательны, отсюда следует, что
$P(A,\bar{B},C)=P(\bar{A},B,C)=P(\bar{A},\bar{B},C)=0$ или $P(\bar{B},C)=P(\bar{A},C)=0$.
Поэтому $P(C)=P(A,C)+P(\bar{A},C)=P(A,C)$ и аналогично $P(C)=P(B,C)$.
✒ Ещё одно двухстороннее следствие $C\to A,~C\to B~~~~\Leftrightarrow~~~~C\to A\,\&\,B~~$ имеет вид:
$$
P(C\to A) = P(C\to B) = 1 ~~~~~~~~~~~~~~\Leftrightarrow~~~~~~~~~~~~~P(C \to A,B) = 1.
$$
Справа-налево оно доказывается при помощи формулы полной вероятности. Так как $P(C\to A,B)=1$, то
$$
P(A,B,C) = P(C)= P(A,B,C) + P(A,\bar{B},C) + P(\bar{A},B,C) + P(\bar{A},\bar{B},C).
$$
Так как все вероятности неотрицательны, отсюда следует, что
$P(A,\bar{B},C)=P(\bar{A},B,C)=P(\bar{A},\bar{B},C)=0$ или $P(\bar{B},C)=P(\bar{A},C)=0$.
Поэтому $P(C)=P(A,C)+P(\bar{A},C)=P(A,C)$ и аналогично $P(C)=P(B,C)$.
Следование слева-направо получается аналогично из $P(A,C)=P(C)$, $P(B,C)=P(C)$, расписыванием по формуле полной вероятности правых и левых частей.
 ✒ Односторонний вывод modus ponens $A,~A\to B~~\Rightarrow~B$:
$$
P(A)=P(A\to B)=1~~~~~~~~~~~\Rightarrow~~~~~~~~~~~P(B)=1
$$
доказывается при помощи полной вероятности $P(B)=P(A,B)+P(\bar{A},B)=1 + P(\bar{A},B)\le 1$,
где учтено, что посылки дают $P(A,B)=1$. Так как вероятности неотрицательны, получаем $P(B)=1$.
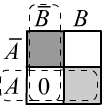
На рисунке приведен графический вывод. Так как $P(A,B)=P(A)=1$ имеем $P(A,\bar{B})=0$, $P(A,B)=1$.
Поэтому и в верхней строке стоят нули. Ненулевая область истинности является подмножеством
истинности $P(B)=1$ (вторая колонка).
✒ Односторонний вывод modus ponens $A,~A\to B~~\Rightarrow~B$:
$$
P(A)=P(A\to B)=1~~~~~~~~~~~\Rightarrow~~~~~~~~~~~P(B)=1
$$
доказывается при помощи полной вероятности $P(B)=P(A,B)+P(\bar{A},B)=1 + P(\bar{A},B)\le 1$,
где учтено, что посылки дают $P(A,B)=1$. Так как вероятности неотрицательны, получаем $P(B)=1$.
На рисунке приведен графический вывод. Так как $P(A,B)=P(A)=1$ имеем $P(A,\bar{B})=0$, $P(A,B)=1$.
Поэтому и в верхней строке стоят нули. Ненулевая область истинности является подмножеством
истинности $P(B)=1$ (вторая колонка).
✒ Кроме вывода modus ponens,
в формальной логике существует множество других нетривиальных
способов получения новых истинных формул.
Очень мощным методом, широко используемом в машинном выводе,
является правило резолюции:
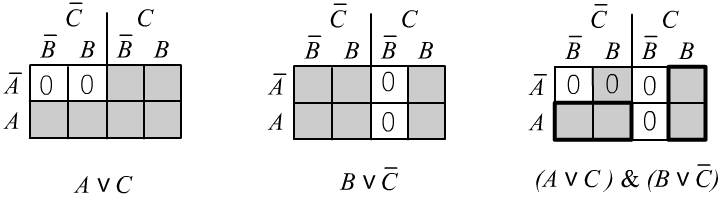
$$
A\vee C,~~~B\vee\bar{C}~~~~\Rightarrow~~~~A\vee B
$$
(посылки истинны, поэтому, если $C\equiv \F $, тогда $A\equiv \T $,
если же $C\equiv \T $, то $B\equiv \T $, и в любом случае $A\vee B\equiv \T $).
Докажем это правило при помощи перечисления интерпретаций:
Аналогично стоит проверить справедливость вывода, использующего свойство транзитивности импликации: $ A\to B,~B\to C~~\Rightarrow~~A\to C, $ которому соответствуют вероятности: $$ P(A\to B) = P(B\to C) = 1 ~~~~~~~\Rightarrow~~~~~~~~P(A\to C) = 1. $$ Впрочем, оно также сразу следует из метода резолюции.
Снова про Алису и Боба
✒ Рассмотрим вероятностный логический вывод в теории про Алису и Боба. Запишем её аксиомы $(\mathbf{A_1})-(\mathbf{A_3})$ в виде: $$ P(l\to \bar{a}\vee \bar{b}) ~=~ P(\bar{l}\to a) ~=~ P(\bar{l}\to b) ~=~ 1. $$ Обратим внимание, что в логике аксиомы типа $\bar{L}\to A$ истинны при любых значениях высказываний $L,\,A$ из области истинных интерпретаций данной теории. В теории вероятностей их необходимо использовать при "семантически верных" конкретных значениях, так как записано выше. В противном случае соотношение $P(\bar{L}\to A)=1$ приводило бы к противоречию: $P(\bar{L}\to a)=P(\bar{L}\to \bar{a})=1$ при $A=a$ и $A=\bar{a}$.
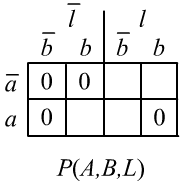 Применяя правило обращения импликации, можно сразу получить:
$$
P( a,b \to \bar{l}) ~=~ P(\bar{a}\to l) ~=~ P(\bar{b}\to l) ~=~ 1,
$$
а из формулы полной вероятности, имеем (большие $A$, $B$ означают любое значение):
$$
P(a,b,l)~=~P(\bar{a},B,\bar{l})~=~P(A,\bar{b},\bar{l}) ~=~ 0.
$$
Таким образом, аксиомы позволяют зафиксировать нулевые совместные вероятности $P(A,B,L)$,
представленные в таблице справа (вероятности интерпретаций), но не дают значения "внелогических вероятностей"
в пустых клетках. Известно только, что их суммарная вероятность равна единице.
Применяя правило обращения импликации, можно сразу получить:
$$
P( a,b \to \bar{l}) ~=~ P(\bar{a}\to l) ~=~ P(\bar{b}\to l) ~=~ 1,
$$
а из формулы полной вероятности, имеем (большие $A$, $B$ означают любое значение):
$$
P(a,b,l)~=~P(\bar{a},B,\bar{l})~=~P(A,\bar{b},\bar{l}) ~=~ 0.
$$
Таким образом, аксиомы позволяют зафиксировать нулевые совместные вероятности $P(A,B,L)$,
представленные в таблице справа (вероятности интерпретаций), но не дают значения "внелогических вероятностей"
в пустых клетках. Известно только, что их суммарная вероятность равна единице.
Однако, логические выводы из посылок, можно проводить как и в булевой логике. Докажем, например, что из $A=a$ и $L=l$ следует $B=\bar{b}$. Для этого воспользуемся методом от противного. Если $P(a,l\to \bar{b})=1$, то по формуле полной вероятности должны иметь $P(a,l\to b)=0$. Действительно: $$ P(a,l \to b) = \frac{P(a,b,l)}{P(a,l)} = 0. $$
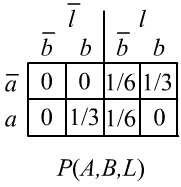 ✒ Теория вероятностей более гибка по сравнению с булевой логикой,
так как позволяет выражать также не единичные вероятности.
Например, пусть известно, что Алиса в гостиной бывает чаще Боба, и вероятность
застать кого-либо в гостинной равна $1/3$:
$$
P(l\to \bar{a}, b) = \frac{1}{2},~~~~~~~~
P(l\to a, \bar{b})=\frac{1}{4},~~~~~~~~
P(l\to \bar{a}, \bar{b})=\frac{1}{4},~~~~~~~~~~P(\bar{l})=\frac{1}{3}.
$$
Вместе с аксиомами, этой информации достаточно, чтобы ответить на любой вопрос.
Соответствующие совместные вероятности приведены в таблице справа.
✒ Теория вероятностей более гибка по сравнению с булевой логикой,
так как позволяет выражать также не единичные вероятности.
Например, пусть известно, что Алиса в гостиной бывает чаще Боба, и вероятность
застать кого-либо в гостинной равна $1/3$:
$$
P(l\to \bar{a}, b) = \frac{1}{2},~~~~~~~~
P(l\to a, \bar{b})=\frac{1}{4},~~~~~~~~
P(l\to \bar{a}, \bar{b})=\frac{1}{4},~~~~~~~~~~P(\bar{l})=\frac{1}{3}.
$$
Вместе с аксиомами, этой информации достаточно, чтобы ответить на любой вопрос.
Соответствующие совместные вероятности приведены в таблице справа.
Например, в бинарной логике из $L,\bar{A}$ нельзя вывести, ни $B$, ни его отрицания $\bar{B}$. Действительно, если в гостиной кто-то есть ($L$) и Алиса не в спальне, то Боб может быть, как с ней, в гостиной, так и в своей спальне (поверьте, что множество истинности $L\,\bar{A}$ не является подмножеством ни $B$, ни $\bar{B}$). В теории вероятностей однозначного вывода сделать, конечно, также нельзя, но допустимо вероятностное рассуждение: $$ P(l,\bar{a}\to b) = \frac{P(\bar{a}, b, l)}{P(\bar{a},l)} = \frac{1/3}{1/2} = \frac{2}{3}. $$ В интервальной логике возможно получение ещё более сильных результатов в условиях неопределённостей.
Вероятности предикатов
В заключение кратко рассмотрим формальную теорию, построенную при помощи предикатов. Как и выше, будем считать, что вероятность аксиомы вида $\forall_x \,A(x)$ равна единице. Если вероятность конъюнкции равна единице, то единице равны вероятности каждого аргумента конъюнкции: $$ P(A(x_1)\,\&\,A(x_2)\,\&\,...) = 1~~~~~~~~~~\Rightarrow~~~~~~~~~~~~\forall_x \,[\,P\bigr(A(x)\bigr)= 1\,]. $$ Таким образом, теоремы $\forall_x\, A(x)$ бинарной логики предикатов имеют единичные вероятности $P\bigr(A(x)\bigr)=1$ для любого предмета теории.
◊ Рассмотрим в качестве примера отношение $(x\,\text{in}\,y)$ из обыденных знаний: объект $x$ находится внутри объекта $y$. Оно удовлетворяет следующим аксиомам строго древесного порядка (кванторы всеобщности опущены): $$ \begin{array}{lll} \neg(x~\text{in}~x) & ~~~~~~ & (1) & \text{антирефлексивность}\\ (x~\text{in}~z)\,\&\,(z~\text{in}~y)~\to~(x~\text{in}~y) & & (2) & \text{транзитивность}\\ (z~\text{in}~x)\,\&\,(z~\text{in}~y)~\to~(x~\text{in}~y)\vee(y~\text{in}~x)\vee(x=y) & & (3) & \text{деревесность} \end{array} $$
Из антирефлексивности и транзитивности следует асимметричность отношения: $$ \begin{array}{lll} (y~\text{in}~x)~\to~\neg (x~\text{in}~y) &~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ & (4) & \text{асимметричность}\\ \end{array} $$ Докажем это при помощи вероятностных методов. Для любых объектов из первых двух аксиом имеем следующие соотношения между вероятностями: $$ P(x~\text{in}~x) = 0,~~~~~~~~~~~~~~~P(x~\text{in}~z,~z~\text{in}~y) = P(x~\text{in}~y). $$ Полагая $y=x$, получаем: $$ P(x~\text{in}~z,~z~\text{in}~x)=0~~~~~~\Rightarrow~~~~~ P\bigr(\,\neg(x~\text{in}~z~\,\&\,~z~\text{in}~x)\,\bigr)=P\bigr(\,\neg(x~\text{in}~z)\vee\neg(z~\text{in}~x)\,\bigr)=1. $$ Отсюда, по правилу единичности импликации, получаем асимметричность: $P\bigr(\,(x~\text{in}~z)~\to~ \neg(z~\text{in}~x)\,\bigr)=1$.
