RL: Q-обучение

Введение

Многие задачи обучения с подкреплением сводятся к марковским процессам. Формально, это означает, что условная вероятность перехода в новое состояние зависит только от текущего состояния, выполненного в нём действия и не зависит от предыдущих состояний и действий: $$ P(s_{t+1}\,r_{t+1}\,|\,...\,s_{t-1},\,a_{t-1},~s_t,\,a_t) = P(s_{t+1}\,r_{t+1}\,|\,s_t,\,a_t). $$ В этом случае будущее определяется настоящим и не требует знания прошлого. Хотя, напомним, что в общем случае состояние может зависеть от нескольких предыдущих наблюдений.

Выбор оптимальной стратегии (policy function) в такой марковской среде называется марковским процессом принятия решения (Markov decision process, MDP). Обсуждаемые в этом документе идеи лежат в основе многих методов обучения с подкреплением.

Простые марковские переходы

Рассмотрим сначала модель в которой нет действий. Среда в дискретные моменты времени из состояния $s$ случайно переходит в очередное состояние $s'$ с вероятностями $P_{ss'}=P(s'|s)$. При попадании в состояние с номером $s'$ начисляется фиксированное вознаграждение $r'$, зависящее от $s'$. В результате получается временная последовательность (нижний индекс - момент времени): $$ s_0 ~\mapsto~ s'_1,r'_1 ~\mapsto ~s''_2,r''_2 ~\mapsto ~...,~~~~~~~s_t \in \mathbb{S},~~r_t \in \mathbb{R}, $$ где $\mathbb{S}$ - множество целых чисел (номера состояний), а $\mathbb{R}$ - множество вещественных чисел (награды). Нас интересует суммарное будущее дисконтированное вознаграждение, полученное после момента времени $t$: $$ R_{t+1} = r_{t+1} + \gamma\,r_{t+2} + \gamma^2\,r_{t+3} + ... ~=~ r_{t+1} + \gamma\, R_{t+2}. $$ Ценностью состояния $V(s)$ называется суммарное дисконтированное вознаграждение, при старте из состояния $s$ в последующих состояниях, усреднённое по всем возможным траекториям: $$ V(s) = \langle R_{t+1}\,|\, s_t = s \rangle. $$ Найдём уравнение, которому должна удовлетворять $V$ - функция.

Уравнение Беллмана

Запишем будущее накопленное дисконтированное вознаграждение в виде: $R_{t+1}=r_{t+1} + \gamma\,R_{t+2}$. Усредним его выражение по траекториям, стартующим из состояния $s_t=s$: $$ V(s) = \langle r_{t+1}+\gamma\,R_{t+2}\,|\, s_t = s \rangle. $$

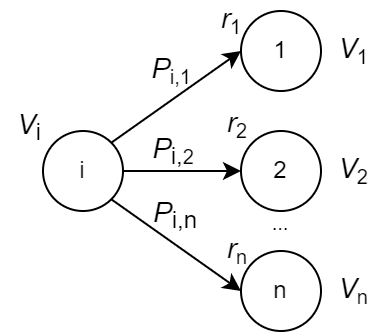
Пусть среда из состояния с номером $i$ может перейти в состояния $1,...,n$. При переходе в $j$-е состояние агент получит вознаграждение $r_j$ (за попадание в него) плюс дисконтированное будущее вознаграждение равное $V_j$ за всю последующую историю (ценность $j$-того состояния). Для получения $V_i$ все эти награды следует усреднить. Для этого умножим их на вероятности переходов $P_{ij}=P(s_{t+1}=j\,|\,s_t=i)$ и просуммируем по $j$: $$ ~~~~~~~~~~~~~~~~~~~V_i = \sum_j P_{ij}\,\cdot\, \bigr(r_{j} + \gamma\,V_j\bigr). $$ Эта система называется уравнением Беллмана. Записав её в матричном виде $\mathbf{V}=\mathbf{P}\cdot(\mathbf{r}+\gamma\,\mathbf{V})$ или $(\mathbf{1} - \gamma\,\mathbf{P})\mathbf{V}=\mathbf{P}\cdot \mathbf{r}$, несложно получить решение: $$ \mathbf{V} = (\mathbf{1} -\gamma\,\mathbf{P})^{-1}\cdot \mathbf{P}\cdot \mathbf{r}, $$ где $(\mathbf{1} -\gamma\,\mathbf{P})^{-1}$ матрица, обратная к матрице $\mathbf{1} -\gamma\,\mathbf{P}$, а $\mathbf{1}$ - единичная матрица.

Пример

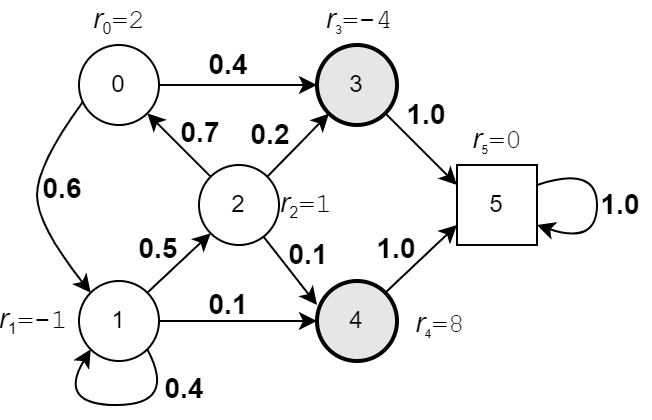
Пусть среда может находится в пяти состояниях, два из которых (3 и 4) терминальные (после них "блуждание" заканчивается). Удобно ввести ещё одно состояние (на рисунке квадрат) при попадании в которое вознаграждения нет и там среда остаётся "навсегда" и награды перестают начисляться (конец блужданиям). Вероятности переходов указаны рядом со стрелками, а вознаграждения - возле состояний.

Запишем вектор вознаграждений и матрицу вероятностей переходов для такой среды: 

import numpy as np

r = np.array(  [2.,  -1.,   1.,  -4.,   8.,   0. ] )
P = np.array([ [0.,   0.6,  0.,   0.4,  0.,   0.,   ],
               [0.,   0.4,  0.5,  0.,   0.1,  0.,   ],
               [0.7,  0.,   0.,   0.2,  0.1,  0.,   ],
               [0.,   0.,   0.,   0.,   0.,   1.0,  ],
               [0.,   0.,   0.,   0.,   0.,   1.0,  ],
               [0.,   0.,   0.,   0.,   0.,   1.0,  ]  ])
Для проверки, стоит убедиться, что сумма P по строкам даёт единицы (вероятности перехода "куда угодно"): 
np.sum(P, axis=1)           # [1. 1. 1. 1. 1. 1.]
Для получения функции полезности состояний, воспользуемся матричным решением уравнения Беллмана c $\gamma=0.9$: 
from numpy.linalg import inv   # получение обратной матрицы
gamma = 0.9
np.dot( inv(  np.eye(len(r)) - gamma*P  ), np.dot(P, r) )
Напомним, что в библиотеке numpy функция dot вычисляет произведение со свёрткой (в данном случае сумма по $j$ от $P_{ij}\cdot r_j$), а eye - это единичная матрица. В результате получаем: 
[-1.195, 1.861, 0.647, 0., 0., 0.]
Ценности терминальных состояний 3,4,5 нулевые (начиная с них агент дальше ничего не получает). Наименее ценное состояние 0, а наиболее ценное - состояние 1.

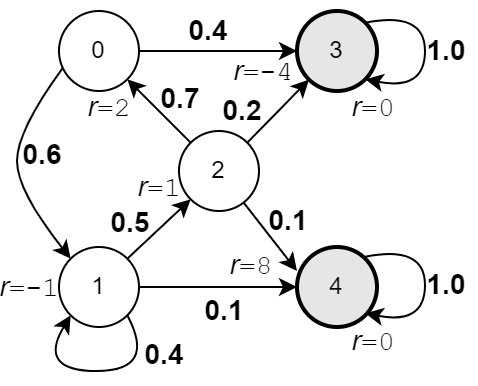Заметим, что можно не вводить фейкового терминального состояния. Однако тогда награды должны быть матрицами $r_{ij}$. Например при переходе из терминального состояния 4 в него же награда будет нулевая $r_{4,4}=0$. В тоже время $r_{1,4}=8$. Уравнение Беллмана в этом случае принимает следующий вид: $$ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~V_i = \sum_j P_{ij}\,\cdot\, \bigr(r_{ij} + \gamma\,V_j\bigr). $$ Предлагается проврить, что решение этого уравнения дают те же значения для ценностей состояний, что были получены выше.

В ещё более общем случае, награды могут быть вероятностными и тогда: $$ V_i = \sum_{j,\,r} P_{i\,j\,r}\,\cdot\, \bigr(r + \gamma\,V_j\bigr), $$ где $P(j,r|i)$ - вероятность перехода из состояния $i$ в состояние $j$ с получением при этом награды $r$.

Монте-Карло моделирование

Найдём ценности состояний этой же среды при помощи Монте-Карло моделирования. Для этого будем много раз запускать блуждание среды начиная с одного и того-же состояния s0, вычисляя по каждому эпизоду полученное вознаграждение: 

states      = np.arange(len(r))             # [0,1,2,3,4,5]
terminals   = [3,4]                         # терминальные состояния
rews, steps = [], []                        # вознаграждения и шагов
s0          = 0                             # стартовое состояние

for _ in range(10000):                      # делаем 10000 экспериментов
    rew, s, discont = 0, s0, 1
    for i in range(100):                    # на всякий случай ограничиваем
        s = np.random.choice(states,p=P[s]) # состояние по распределению P[s]

        rew += r[s] * discont               # накапливаем вознаграждение
        discont *= gamma                    # сильнее дисконтируем

        if s in terminals:                  # попали в терминальное состояние
            break                           # дальше вознаграждение не меняется

    rews.append(rew)                        # сохраняем вознаграждение
    steps.append(i+1)                       # сохраняем число сделанных шагов

print("V(%d) =  %7.2f ± %5.4f  T(%d): %7.2f ± %5.4f"
      % (s0, np.mean(rews),  np.std(rews) /len(rews)**0.5,
         s0, np.mean(steps), np.std(steps)/len(steps)**0.5))
В результате получится что-то типа: 
V(0) = -1.19 ± 0.04    V(1) =  1.84 ± 0.04     V(2) =  0.63 ± 0.04
T(0) =  3.88 ± 0.04    T(1) =  4.67 ± 0.04     T(2) =  3.66 ± 0.04
Ошибка убывает как $\sigma/\sqrt{N}$, где $\sigma$ - стандартное отклонение std, а $N = 10000$ - число экспериментов. В рамках этой ошибки результаты моделирования совпадают с точными значениями, полученными при помощи уравнения Беллмана.

Функция политики

Перейдём теперь к более типичной для обучения с подкреплением задаче. Пусть в состоянии с номером $i$ агент с вероятностью $\pi_{i\alpha}=\pi(\alpha\,|\,i)$ совершает действие с номером $\alpha$ (ниже латинские индексы используются для номеров состояний, а греческие - для действий). В результате действия агента среда переходит в состояние под номером $j$ с вероятностью $P_{i\alpha j}=P(j\,|\,i,\alpha)$, получая в нём награду $r_j=r(s_j)$.

Ценности состояний по-прежнему удовлетворяют уравнению Беллмана: $$ V_i = \sum_j \tilde{P}_{ij}\, \bigr(r_j + \gamma\,V_j\bigr),~~~~~~~~~~~~\tilde{P}_{ij} = \sum_\alpha \pi_{i\alpha}\,P_{i\alpha j}, $$ где $\tilde{P}_{ij}$ вероятности перехода из $i$ в $j$ равны произведению вероятности сделать в состоянии $i$ действие $\alpha$ на вероятность перейти после этого в состояние $j$ с суммой по всем возможным действиям.

Найдём уравнение для Q-функции полезности действия $a$, совершённого в состоянии $s$: $$ Q(s,a) ~=~ \langle R_{t+1}\,|\,s_t=a,\,a_t=a\rangle. $$ Для дискретного случая это будет матрица $Q_{i\alpha}$. Зная её, можно вычислить полезность состояния (при совершении любого действия с вероятностями $\pi_{i\alpha}$): $$ V_i = \sum_\alpha \pi_{i\alpha} \, Q_{i\alpha}. $$ Можно также записать обратную связь. Ценность действий $Q_{i\alpha}$ в состоянии $i$ равна среднему вознаграждению при непосредственном переходе в состояние $j$, плюс дисконтированные будущие вознаграждения состояний, в которые среда попадает при таком переходе: $$ Q_{i\alpha} = \sum_{j}P_{i\alpha j}\,(r_j + \gamma\,V_j\bigr). $$ Подчеркнём, что полезности состояний $V$ и действий $Q$ зависят от выбранной агентом политики (матрицы вероятностей $\pi_{i\alpha}$). Изменение политики меняет и эти функции. Кроме этого, вычисления по приведенным формулам возможны только, если известна модель среды, т.е. вероятности переходов $P_{i\alpha j}$ и получаемые вознаграждения $r_j$.

Вычисления на numpy

Сгенирим случайный набор вероятностей переходов между состояниями (при совершении действия) для некоторой среды с десятью состояниями и тремя возможными дискретными действиями агента в каждом состоянии. Политику агента $\pi_{i\alpha}$ также заполним случайными значениями: 

num_states, num_actions = 10, 3                          # состояний и действий

pi = np.random.random((num_states, num_actions))         # вероятности действий
pi = pi/np.sum(pi, axis=1).reshape(-1,1)                 # нормируем на единицу

P = np.random.random((num_states,num_actions,num_states))# модель среды
P = P/np.sum(P, axis=2).reshape(num_states,num_actions,1)# нормируем

r  = np.linspace(-10, 10, num_states)                    # награды [-10...10]
Полученные матрицы имеют формы (10, 3), (10, 3, 10) и (10,) соответственно. Суммирование np.sum(pi, axis=1) даёт вектор единиц (вероятность совершить любое действие) и np.sum(P, axis=2) - это матрица (10, 3) с единичными элементами.

Вычислим вероятности $\tilde{P}_{ij}$: 

piP = np.sum( np.expand_dims(pi, axis=2) * P, axis=1)
Функция expand_dims добавляет в тензор ещё одну ось, делая для pi размерность (10, 3, 1). Произведение на P даёт тензор размерности (10, 3, 10) = (10, 3, 1)*(10, 3, 10). При этом включается механизм расширения (broadcasting) при котором тензор (10, 3, 1) дублируется 10 раз, после чего уже перемножаются элементы тензоров. Финальное суммирование по первой оси даёт матрицу (10, 10).

Теперь по приведенным выше формулам, несложно найти полезности состояний и действий: 

V = np.dot( inv(  np.eye(len(r)) - gamma*piP  ), np.dot( piP, r) )
Q = np.dot(P, r + gamma*V)
Для проверки, можно также вычислить: np.sum(pi * Q, axis=1) и убедиться, что снова получается V.

Все приведенные выше примеры можно найти в этом нотбуке.

Стратегии жадные и не очень

Разные политики $\pi(a|s)$ приводят к различным $Q$ и $V$ функциям. Из всех возможных политик оптимальной будет та, для которой значения ценности состояний и действий максимальны: $$ V^*(s) = \arg\max_\pi V^\pi(s),~~~~~~~~~~~~~~~~~ Q^*(s,a) = \arg\max_\pi Q^\pi(s,a). $$ В свою очередь, если известна оптимальная $Q^*$-функция несложно записать оптимальную детерминированную политику: $$ a=\pi^*(s) = \arg\max_a Q^*(s,a). $$

В процессе обучения (пока $Q$ известна плохо) такую детерминированную политику можно рандомизировать, выбрав параметр $\epsilon \in [0...1]$ и равномерно распределённое случайное число $p\in [0...1]$: $$ a = \left\{ \begin{array}{l} \displaystyle\arg\max_a Q(s,a) & p > \epsilon\\ \displaystyle\mathrm{any} & \mathrm{else} \end{array}\right. $$ Если $\epsilon=0$ то всегда выбирается оптимальное действие. При $\epsilon=0.5$ в половине случаев будет выбираться случайное действие. По мере обучения $\epsilon$ уменьшается. Это позволяет на начальных этапах агенту больше "экспериментировать".

Вместо $\epsilon$-стратегии действие можно также выбирать с вероятностями пропорциональными их полезности. Для этого используется функция softmax по индексу $\alpha$: $$ \pi_{i\alpha} = \mathrm{soft}( Q_{i\alpha} - \bar{Q}_{i\alpha}),~~~~~~~~~~ \mathrm{soft}(x_\alpha) = \displaystyle \frac{e^{x_\alpha}}{\sum_\beta e^{x_\beta}}, $$ где среднее $\bar{Q}_{i\alpha}$ (также по индексу $\alpha$) вычитается, чтобы не произошло переполнения при вычислении экспонент. На Python это выглядит следующим образом: 

from scipy.special import softmax  # импортируем функцию softmax
 
Q  = np.random.uniform( size=(num_states, num_actions) )
 
aQ = Q.mean(axis=1, keepdims=True) # средние значения (num_states, 1)
pi = softmax(Q - aQ, axis=1)       # условные вероятности pi(a|s)
 
s  = 1                             # номер состояния
a  = np.random.choice(np.arange(num_actions), p=pi[s])

Максимизация Q-функции

Пусть агент выбирает действие, соответствующее его максимальной полезности $a = \arg\max_a Q(s,a)$ и всегда ей следует. Тогда: $$ V_i = \sum_\alpha \pi_{i\alpha}Q_{i\alpha} = \max_\alpha Q_{i\alpha}, $$ так как все вероятности политики равны нулю, кроме того действия, для которого $Q_{i\alpha}$ максимальна. Поэтому, уравнение Беллмана $Q_{i\alpha} = \sum_{j}P_{i\alpha j}\,(r_j + \gamma\,V_j\bigr)$ для полезности действий в оптимальной стратегии приобретает вид: $$ Q_{i\alpha} = \sum_j P_{i\alpha j}\, (r_j + \gamma \,\max_\beta Q_{j\beta}). $$

Даже, если модель среды ($P_{i\alpha j}$, $r_i$) известна, непосредственно это уравнение решить нельзя. Однако можно воспользоваться итерационным методом: $$ Q^{\mathrm{new}}_{i\alpha} = Q_{i\alpha} + \lambda \bigr[\sum_j P_{i\alpha j}\, (r_j + \gamma \,\max_\beta Q_{j\beta}) - Q_{i\alpha}\bigr], $$ где $\lambda$ - гиперпараметр (скорость обучения). Смысл этого соотношения прост. Если $Q_{i\alpha}$ меньше, чем требуемое по уравнению Беллмана значение, то её необходимо немного увеличить, а если больше - то уменьшить. Параметр $\lambda$ регулирует степень изменения $Q_{i\alpha}$ на каждой итерации.

Метод Q-обучения

Если модель среды неизвестна, используют Монте-Карло моделирование, в процессе которого подправляют значения $Q_{i\alpha}$. При этом, для исследования пространства состояний применяется $\epsilon$-жадная стратегия с убывающим $\epsilon$: $$ a ~=~\pi_\epsilon(s) ~=~ \mathrm{any}~~\mathbf{if}~~p < \epsilon~~\mathbf{else}~~\arg\max_a Q(s_t,a). $$ Тогда на каждом шаге моделирования производится вычисление: $$ \begin{array}{l} \displaystyle a_t = \pi_\epsilon(s_t)~~~~\mapsto~~~~~~s_{t+1},~r_{t+1}\\[2mm] \displaystyle Q^\mathrm{new}(s_t,a_t) = Q(s_t,a_t) + \lambda\,\bigr[r_{t+1}+\gamma \,\max_a Q(s_{t+1}, a)-Q(s_t,a_t)\bigr]. \end{array} $$ Выражение в квадратных скобках называется temporal difference (TD) и обычно обозначается символом $\delta$. Если $\delta > 0$, то переход $s,a\mapsto s',r'$ является позитивно неожиданным, а если $\delta < 0$ - то негативно неожиданным.

Приведём соответствующий код. Параметр жадности $\epsilon$ будем начинать со значения eps1, экспоненциально уменьшая его до значения eps2 в течении decays эпох, после чего положим $\epsilon=0$. 

Q = np.zeros( (num_states, num_actions) )  # начальные значения 0

eps1, eps2, decays = 1, 0.001, 50000       # параметры epsilon-распада
epsilon = eps1
decay   = math.exp(math.log(eps2/eps1)/decays)

def policy(s):                             # epsilon-жадная политика
    if np.random.random() < epsilon:       # случайно любое действие
        return np.random.randint(n_actions)
    return np.argmax(Q[s])                 # иначе лучшее
Собственно алгоритм Q-learning содержится в функции run_episode: 
def run_episode(ticks=1000):
    s0 = env.reset()                       # начальное состояние среды
    for _ in range(ticks):               
        a0 = policy(s0)                    # выбираем действие
        s1, r1, done = env.step(a)         # новое состояние и награда

        Q[s0, a0] += lm * ( r1 + gamma * np.max(Q[s1]) - Q[s0,a0] )

        if done:                           # терминальное состояние
            return

        s0 = s                             # продолжаем с нового состояния

def learn(episodes, ticks):
    for episode in range(episodes):        # проходы по эпизодам
        run_episode(ticks)
        
        epsilon *= decay                   # становимся жаднее
        if epsilon < eps2: epsilon = 0
Такой итерационный метод называется Q-learning. Это типичный пример онлайн (online) обучения, когда обучение происходит на каждой новой полученной порции данных.

Метод SARSA

Аналогичная итерационная процедура без вычисления максимума называется метод SARSA (State-Action-Reward-State-Action): $$ \begin{array}{l} \displaystyle a_t = \pi_\epsilon(s_t)~~~~~~\mapsto~~~~~s_{t+1},~r_{t+1}~~~~~\mapsto~~~~~\displaystyle a_{t+1} = \pi_\epsilon(s_{t+1})\\[2mm] \displaystyle Q^\mathrm{new}(s_t,a_t) = Q(s_t,a_t) + \lambda\,\bigr[r_{t+1}+\gamma \,Q(s_{t+1}, a_{t+1})-Q(s_t,a_t)\bigr]. \end{array} $$ Ниже приведен код реализации алгоритма: 

def run_episode(ticks=1000):    
    s0 = env.reset()
    a0 = policy(s0)
    for t in range(ticks):                
        s1, r1, done, _ = env.step(a0)
        a1 = policy(s1)
                        
        Q[s0, a0] += lm * (r1 + gamma * Q[s1, a1] -  Q[s0, a0])
                
        if done:           
            return
            
        s0, a0 = s1, a1

Если $\epsilon=0$ (жадная стратегия) $Q$-learning и SARSA совпадают, так как $Q(s_{t+1}, a_{t+1})$ равна $\max_a Q(s_{t+1}, a)$. Однако это не так при $\epsilon > 0$. Различие довольно тонкое, но важное.

Метод $Q$-learning называют off-policy обучением. Это означает, что выбор действия осуществляется при помощи одной политики ($\epsilon$-жадной), а при итерационном вычислении $Q$-функции используется другая (оптимальная политика). Т.е. $Q$-функция "предполагает", что использовалась жадная политика, тогда как это на самом деле не так (при $\epsilon > 0$).

Соответственно метод SARSA называют on-policy обучением, т.к. $Q$-функция оценивается на той-же политике, при помощи которой было выбрано действие, т.к. в $Q(s_{t+1}, a_{t+1})$ стоит конкретное действие, которое выдала политика $\pi_\epsilon(s_{t+1})$.

Итерационный поиск политики

Методы $Q$-learning и SARSA хороши тем, что не требуют знания модели среды, т.е. вероятностей переходов $P(s',r'|s,a)$. Если такая модель известна, можно воспользоваться простым итерационным алгоритмом уточнения политики (policy iteration algorithm). В этом алгоритме сначала задаётся некоторая детерминированная политика $a=\pi(s)$ (она обычно инициализируется случайными значениями). На её основе вычисляется $V$-функция. Затем, с её помощью строиться уточнённая (улучшенная политика) и вычисления повторяются. Таким образом имеем два, повторяющихся этапа:

1. Оценка политики (policy evaluation). Итерационно вычисляем для всех состояний, пока с некоторой точностью функция ценности не перестанет изменяться: $$ V_{k+1}(s) = \sum_{s',r'} P(s',r'\,|\,s,a)\, \bigr[r'+\gamma\,V_k(s')\bigr],~~~~~~~~~a=\pi(s). $$ В принципе, можно использовать два массива для $k$-той итерации $V_k$ и для следующей $V_{k+1}$ и затем менять их местами. Однако хорошо работает и "in-place" обновление при котором для некоторых состояний уже используется улучшенное значение ценности.

2. Улучшение политики (improving the policy) при котором вычисляется политика на основании жадной стратегии: $$ \pi(s) = \arg\max_a Q(s,a) = \arg\max_a \sum_{s',r'} P(s',r'\,|\,s,a) \,\bigr[r'+\gamma\,V_k(s')\bigr]. $$ Снова повторяем первый этап до тех пор, пока политика не перестаёт изменяться.

Пример: Frozen Lake

Рассмотрим в качестве простого примера среду Frozen Lake из набора сред OpenAI Gym. Есть квадратная неизменная карта замёршего озера, часть ячеек которого содержит проруби. Необходимо провести гнома из левого верхнего угла карты (стартовое состояние) в правый нижний (целевое состояние) не провалившись в прорубь. Проблема в том, что гном не вполне трезвый и его шатает вправо-влево. Поэтому на скользком льду (в режиме is_slippery=False по умолчанию) он с вероятностью 1/3 сместиться туда, куда планирует, а с вероятностями 1/3 сдвинется в одно из перпендикулярных направлениях. При попытке выйти за карту гном останется на прежней ячеке (или его шатнёт в одно из перпендикулярных направлений).

Таким образом, есть 16 состояний (номера ячеек) и 4 действия (0: LEFT, 1: DOWN, 2: RIGHT, 3: UP). При попадании в прорубь или в целевую ячейку эпизод оканчивается. При достижении целевой ячейки даётся награда 1, иначе награда 0. Среда FrozenLake сильно стохастична и имеет очень скудную награду (только при удачном конце эпизода).

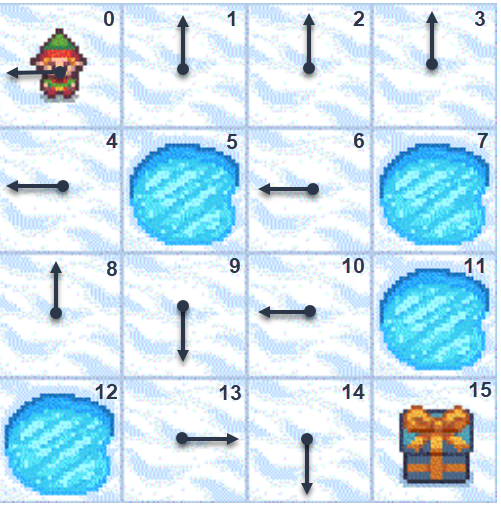Оптимальная политика, приведенная на рисунке справа, может показаться неожиданной. Однако, с учётом стохастичности среды она разумна. Рассмотрим, например, состояние 6. Если бы пьяный гном попытался сместится вниз, это бы у него получилось бы только с вероятностью 1/3, а с вероятностью 2/3 он бы оказался в одной из соседних прорубей. А при движении влево его с вероятностью 1/3 качнёт вниз (куда нужно), а в прорубь он провалится уже с вероятностью 1/3. Следуя такой политики, гном гарантированно (хотя с возвратами) пройдёт ячейки 0,4,8,9, после чего его маршрут может разветвится и в том числе зациклиться. 

def policy(s):
    return [0,3,3,3, 0,0,0,0, 3,1,0,0, 0,2,1,0][s]

Из вероятностных соображений несложно вычислить V-функцию при оптимальной стратегии. Например, для состояния 0 имеем $V_0=(1/3)\,V_0+(1/3)\,V_0+(1/3)\,V_4$, а для состояния 14 при $\gamma=1$ имеем $V_{14}=(1/3)\,V_{14}+(1/3)\,V_{13}+(1/3)(1+0)$. Записывая подобные соотношения для состояний 0, 1, 2, 3, 4, 8, 9, 13, 14, 6, 10, получаем следующую матрицу: $$ V(s) = \frac{1}{17}\, \begin{pmatrix} 14 & 14 & 14 & 14 \\ 14 & 0 & 9& 0 \\ 14 & 14 & 13 & 0 \\ 0 & 15 & 16 & 0 \\ \end{pmatrix} $$

Оба метода Q-learning и SARSA неплохо справляются с этой задачей за 10000 эпизодов. При этом методы очень неустойчивы при gamma=1 и не сходятся при малых decays. В этой задаче награда выдаётся только в целевом состоянии. Пока агент его не достигнет матрица $Q(s,a)$ будет оставаться нулевой. Только после первого попадания в цель, начнётся "обратное" распространение значений по $Q(s,a)$, пока она не стабилизируется. Поэтому в данном случае использование $\epsilon$-стратегия необходимо.

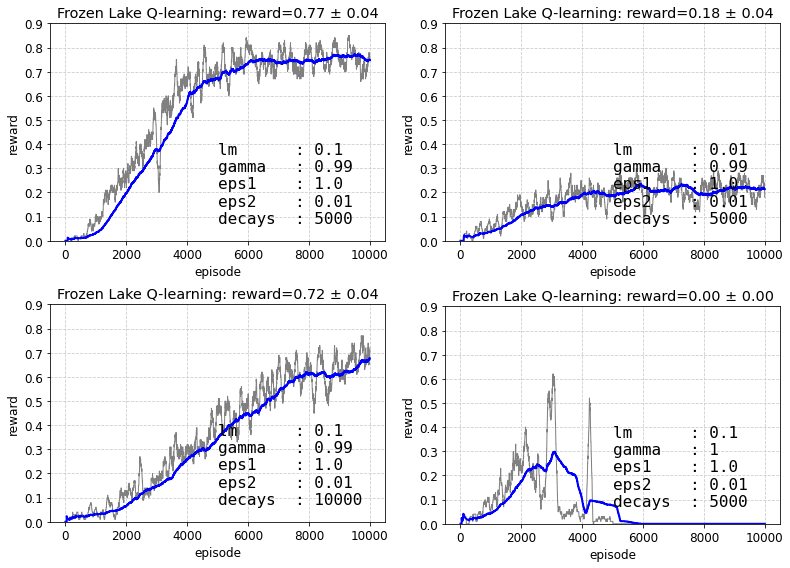
Типичная средняя награда 0.74 означает, что пьяному гному не удаётся добраться до цели в четверти случаев. Почему это значение несколько ниже теоретического 14/17 = 0.8235 я не знаю.

Ниже приведены значения Q, V функций и политика агента. Кликните на картинку, чтобы увидеть обучение в динамике. Первый триста кадров соответствуют эпизодами 100-300, затем кадры идут с шагом в 500 эпизодов.

Задачи

1. Доказать, что ценность состояния $V(0)$ марковской среды, приведенной на рисунке равна $r\,p/(1-\gamma\,p)$. Проделать это следующими способами:

  1. Получить из вероятностных соображений, вычислив среднюю награду.
  2. Записать уравнение Беллмана и решить его как систему линейных уравнений.
  3. Найти обратную матрицу $(1-\gamma\,\mathbf{P})^{-1}$ и вычислить $V(s)$ в матричном виде.

2. Изучить среду Frozen Lake, применив к ней методы Q-learning и SARSA

  1. Начать без скольжения env = gym.make("FrozenLake-v1", is_slippery=False).
  2. Тоже со скольжением env = gym.make("FrozenLake-v1"). Построить кривые обучения.
  3. Изучить свойства гиперпараметров дисконтирования decays, gamma, lm,