RL - обучение с подкреплением

Постановка задачи

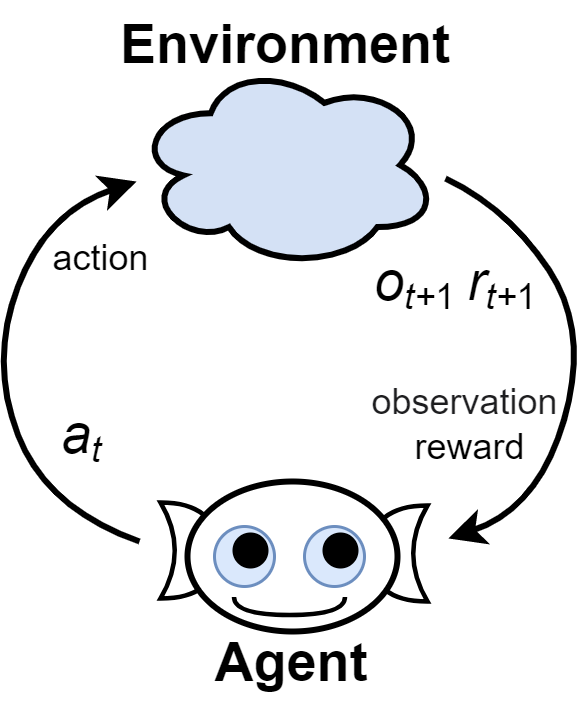
Обучение с подкреплением (Reinforcement Learning, RL) - набор методов, позволяющих агенту (интеллектуальной системе) вырабатывать оптимальную стратегию при его взаимодействии со средой (внешним миром).

В каждый (обычно дискретный) момент времени $t$ агент может оказать на среду некоторое воздействие (action) $a_t$. В ответ он получает информацию - наблюдение (observation) $o_{t+1}$, полностью или частично характеризующее новое состояние среды (state) $s_{t+1}$ и числовую характеристику успешности действий, называемую наградой (reward) $r_{t+1}$. $$ o_0 ~\overset{a_0}{\rightarrow}~ \{ o_{1},\,r_{1} \} ~ \overset{a_1}{\rightarrow}~ \{o_{2},\,r_{2}\}~ \overset{a_2}{\rightarrow}~... $$ На основе полученной к моменту времени $t$ информации $\{...;~o_{t-2},\,a_{t-2};~o_{t-1},\,a_{t-1};~o_{t},\_\}$ (траектории), агент должен выбрать очередное действие $a_t$ так, чтобы максимизировать накопленное вознаграждение $R=r_1+r_2+...$ за достаточно большой промежуток времени.

Среда (environment) может быть детерминированной или стохастической; с полным или неполным описанием; стационарной или нестационарной. Если среда нестационарна, то её свойства изменяются со временем. Неполное описание означает, что наблюдение $o_t$ несёт не всю информацию о среде (есть "скрытые переменные"). При полном описании наблюдение эквивалентно состоянию среды: $s_t = o_t$. Наконец, в стохастической среде, даже при полном описании, существуют случайные факторы. Начиная из одного и того же состояния и совершив одинаковую последовательность действий, можно получить различные траектории.

В среде могут быть терминальные состояния, при достижении которых "игровой" эпизод оканчивается. Обычно, эпизоды имеют также ограничение по времени (конечное число временных шагов). Наблюдение это, обычно, вектор с вещественными или целочисленными компонентами.

Возможные действия $a_t$ могут принадлежать конечному множеству целых чисел (0 - шаг влево или 1 - шаг вправо) или быть вектором вещественных чисел: {скорость шага, угол поворота}. Многие методы способны работать только с дискретными действиями или только с непрерывными действиями.

В типичных задачах RL вознаграждение $r_{t+1}$ часто не связано непосредственно с действием $a_t$. Отличное от нуля вознаграждение может поступать редко, запаздывать и возникать только после серии негативных значений (долго страдал, но затем много получил). Иногда вознаграждение приходит только в конце (например, при игре в го). Вознаграждение может быть всегда отрицательным. Например, если задачу нужно решить за минимальное время, на каждом шаге будет даваться вознаграждение $r_t = -1$. Максимизация суммарного вознаграждения означает минимизацию времени достижения терминального состояния.

Модель среды

Обычно вместо наблюдения за средой $o_t$, мы будем говорить о её состоянии $s_t$. Следует помнить, что в общем случае эти величины могут не совпадать. Для среды с полным описанием $s_t=o_t$. При неполном описании нужно учитывать историю наблюдений и действий. Даже при учёте всей траектории ${s_0,a_0,\,s_1,a_1,\,...}$, состояние среды может быть вероятностно или вообще оказаться "вещью в себе". Так, пусть для "сжатия" истории наблюдений используется рекуррентная сеть: $$ o_{t+1} = g(s_t;~ o_t, a_t),~~~~~~~~s_{t+1} = f(s_t;~ o_t, a_t). $$ Тогда "вспомогательный" вектор памяти $s_{t}$ естественно интерпретировать как состояние среды.

В процессе обучения агент может формировать модель среды, которая предсказывает вероятность следующего наблюдения на основании траектории: $P(s_{t+1},\,r_{t+1}\,|\,...,s_t,\,a_t)$. Если награда определяется только состоянием, то модель это: $P(s_{t+1},|\,...,s_t,\,a_t)$ и $r_{t} = r(s_t)$.

Если текущее состояние среды $s_t$ содержит всю информацию, необходимую для принятия решения, то такая среда называется марковской. Формально, это означает, что условная вероятность перехода в новое состояние зависит только от текущего состояния и действия: $$ P(s_{t+1},\,r_{t+1}\,|\,...,s_{t-1},\,a_{t-1},~s_{t},\,a_{t}) = P(s_{t+1},\,r_{t+1}\,|\,s_t,\,a_t). $$ В этом случае будущее определяется настоящим и не требует знания прошлого. Выбор оптимальной стратегии в такой среде называется марковским процессом принятия решения (Markov decision process, MDP).

Если наблюдение не даёт всей информации о состоянии (неполное описание, частичная наблюдаемость), то решения в такой среде называется частично наблюдаемым марковским процессом принятия решения (partially observable Markov decision process, POMDP).

Политика агента

Алгоритм по которому агент выбирает действие, принято называть его политикой. Это может быть обычная (детерминированная) функция $a_t=\pi(s_t)$ (policy function), где в качестве аргумента выступает текущее состояние. В $s_t$ могут также включаться предшествующие действия и награды.

Для изучения среды агент должен постоянно "экспериментировать". Даже в стационарной среде с полным описанием, эксперименты нужны, чтобы не "застрять" в некоторой области пространства состояний, т.к. возможно есть более "доходные" состояния среды. Поэтому в общем случае политика - это условная вероятность $\pi(a|s)$ выбора агентом действия $a$ в состоянии $s$.

Детерминированную функцию политики несложно превратить в вероятностную. Например, с вероятностью $p$ выбирается оптимальное (к данному моменту обучения) действие $a=\pi(s)$, а с вероятностью $1-p$ - равновероятно любое другое состояние. Если множество действий дискретно, можно, например, аппроксимировать $\pi(a|s)$ нейронной сетью с числом выходов равных числу возможных действий на которых будет (после softmax) распределение вероятностей соответствующего решения.

Отсутствие обучающих данных

Важное отличие обучения с подкреплением от стандартного обучения с учителем - это отсутствие обучающих данных вида $\{(s,a),~(s',a'),~...\}$, где $a$ - "известные учителю" оптимальные действия, которые необходимо выполнить, когда среда находится в данном состоянии. Агент должен решить задачу, даже если человек не знает как её решать (не знает какие действия оптимальны).

Есть и технические сложности. Так, пусть функция политики $\pi_\theta(a|s)$ аппроксимируется нейронной сетью с параметрами $\theta$ и мы хотим получить максимальное среднее суммарное вознаграждение $\bar{R} = \langle r_1+r_2+... \rangle$ по большому числу конечных эпизодов. В принципе, это стандартная задача оптимизации. При данной политике среднее вознаграждение $\bar{R}$ также является функцией параметров и задача состоит в поиске экстремума: $$ \theta^* = \arg\max_\theta \bar{R}(\theta). $$

Когда параметров немного, можно применять классические методы оптимизации (Nelder-Mead, Powell и т.п.). Если параметров больше, могут сработать стохастические методы типа генетических алгоритмов или отжига. Однако для глубокого обучения эти подходы оказываются практически бесполезными в силу очень большого числа параметров. Эффективные в этом случае градиентные методы напрямую не применимы, так как отсутствует математическая модели среды (для агента она "чёрный ящик"). Это не позволяет вычислить производные целевой функции $\bar{R}(\theta)$ по параметрам $\theta$ и требуются различные трюки, которые и составляют суть обучения с подкреплением.

Примеры RL-задач

При помощи обучения с подкреплением было решено множество сложных задач. Всплеск интереса к этой деятельности начался после того, как компания DeepMind смогла применить глубокое обучение к принятию решений в компьютерных играх Atari по эффективности сравнимой с типичным игроком-человеком (2013). Из последних достижений - наиболее известна система AlphaGo (от той же компании), которая смогла победить чемпиона мира по игре в Го (2016). Рассмотрим несколько типичных для RL задач.

Многорукий бандит

Есть набор одноруких бандитов - игральных автоматов с ручкой. Когда агент дёргает за ручку автомата, он может получить награду.

У каждого автомата своё (неизвестное) распределение вероятностей выигрышей: $P(r|a)$. Задача агента, как обычно, получить максимальное суммарное вознаграждение. В этой задаче наблюдений нет. Действие агента - целые числа, равные номеру автомата за ручку которого агент дёргает на данном шаге.

Это классическая учебная задача на которой, обычно, иллюстрируют баланс между исследованием (exploration) и применением (exploitation). Если агент сначала последовательно дёрнет за за ручку каждого автомата, а затем будет дёргать только за те, что выдали наибольшую награду, то скорее всего он не получит максимального среднего дохода за длительный период времени. В начале обучения ему необходимо изучать среду (оценивать вероятности и награды), чтобы выработать оптимальную стратегию. Например, возможно есть автоматы, которые с малой вероятностью выдают очень большую награду.

Простейший разумный метод, это вычислять ценность действия $Q_t(a)=\langle r(a)\rangle_t$, равную среднему доходу $a$-того автомата, который он принёс к текущему моменту времени $t$. При выборе действия следует использовать эпсилон-жадную стратегию. Для этого задаётся параметр $\epsilon \in [0...1]$. С вероятностью $\epsilon$ автомат выбирается случайно, а с вероятностью $1-\epsilon$, дёргают за ручку наиболее доходного автомата: $$ a_t = \left\{ \begin{array}[ll] \displaystyle случайное~действие,&~~~~~с~вероятностью~ \varepsilon\\ \displaystyle \arg\max_a Q_t(a), &~~~~~с~вероятностью~ 1-\varepsilon \end{array} \right. $$ По мере стабилизации $Q_t(a)$, параметр $\epsilon$ уменьшается. С теоретической точки зрения задача интересна тем, что в ней можно доказать множество теорем об эффективности различных методов.

Frozen Lake

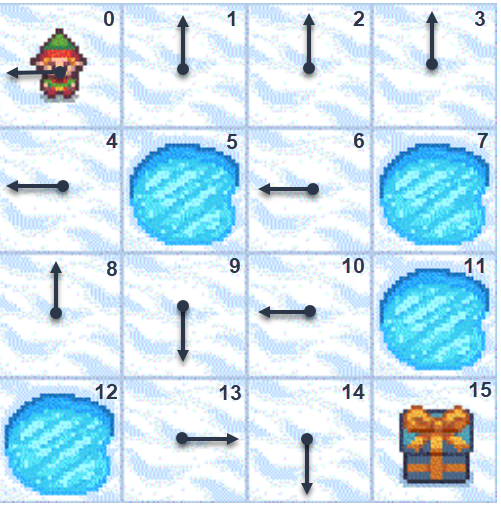Есть квадратная неизменная карта замёршего озера, часть ячеек которого содержит проруби. Необходимо провести гнома из левого верхнего угла карты (стартовое состояние) в правый нижний (целевое состояние) не провалившись в прорубь. Гном не вполне трезвый и его шатает вправо-влево. Поэтому с вероятностью 1/3 он сместиться туда, куда планирует агент, а с вероятностями 1/3 сдвинется в одно из перпендикулярных направлений. При попытки выйти за карту, гном останется на прежней ячеке (или его шатнёт в одно из перпендикулярных направлений).

Таким образом, есть 16 дискретных состояний (номера ячеек) и 4 дискретных действия (0: LEFT, 1: DOWN, 2: RIGHT, 3: UP). При попадании в прорубь или в целевую ячейку эпизод оканчивается. При достижении целевой ячейки (терминальное состояние) даётся награда 1, иначе награда 0. Среда FrozenLake имеет полное описание $o_t=s_t$ (агент знает номер ячейки на которой находится гном), однако сильно стохастична и имеет очень скудную награду (только в конце). На рисунке стрелками показаны оптимальные действия гнома, которые предлагается объяснить в качестве несложной задачи.

CartPole

В качестве среды выступает стержень, прикреплённый шарниром к тележке, которая движется без трения по рельсу. В начальном состоянии стержень расположен вертикально (с небольшим случайным отклонением) и под действием силы тяжести стремится развернуться вниз. Задача состоит в том, чтобы предотвратить падение стержня толкая тележку вправо или влево (кликните мышью на изображение).

В этой задаче наблюдение - это четыре физических параметра: $o_t=\{x,\,\,v,\,\phi,\,\omega\}$, где $x$ - положение тележки, $v$ - её скорость, $\phi$ - угол отклонения стрержня от вертикали, $\omega$ - угловая скорость стержня. Действия агента бинарны: толкнуть тележку вправо ($a=1$) или влево ($a=0$). После каждого действия получается вознаграждение $r=1$ до тех пор, пока угол $|\phi| < 12^\circ$ и тележка находится внутри экрана. В противном случае эпизод оканчивается. Таким образом, задача агента состоит в выборе действий удерживающих стержень вертикально, как можно долго.

Среда CartPole имеет полное описание и оптимальное действие агента полностью определяется текущим наблюдением $s_t=o_t$. Если из наблюдения за средой убрать скорости: $o_t=\{x,\,\phi\}$, то среда будет иметь неполное описание. Для её качественного решения в этом случае необходимо учитывать два последовательных наблюдения: $s_t = \{o_t,\, o_{t-1}\}$.

MountainCar

В этой среде машинка находится между двумя холмами различной высоты. Наблюдение состоит из положения и скорости машинки $o_t=\{x,\,\,v\}$. Агент может толкнуть машинку вправо ($a=2$), ничего не делать ($a=1$) или толкнуть машинку влево ($a=0$). В результате этих действий необходимо забраться на правый (более высокий) холм. При достижении левой границы экрана машинка останавливается (неупругое столкновение). За действия даётся одинаковое вознаграждение $r=-1$ и эпизод заканчивается когда машина достигает цели (флаг на рисунке).

При постоянном выборе действия $a=2$ (к цели), в общем случае, машинке не хватит "мощности" чтобы вскарабкаться на правый холм. Поэтому агенту необходимо раскачивать машинку влево-вправо пока она не наберёт достаточной скорости, чтобы докатиться до цели. Делать это необходимо оптимально, для минимизирования общего времени (числа действий), затраченного на решение (кликните на картинку).

Это детерминированная задача с полным описанием. Она заметно сложнее предыдущей. Если при случайном выборе действия в CartPole можно некоторое время удерживать стержень, то в этой среде случайные действия практически никогда не позволяют достичь вершины. Так как время эпизода ограничено 200-ами интервалами, в большой области пространства параметров целевое суммарное вознаграждение не меняется (равно -200). Соответственно, отсутствуют ориентиры того, где находится оптимум среднего вознагарждения. Кроме этого, неправильные действия в CartPole сказываются быстро, а в MountainCar их эффект "отложен" до конца эпизода.

Pong

Игра Pong - это классическая игра из коллекции Atari games в которой необходимо двигать ракетку вверх-вниз чтобы отражать летающий между игроками теннисный мячик. В рамках коллекции OpenAI Gym в качестве среды выступает изображение 210 x 160 пикселей. Если шарик проходит мимо ракетки противника агент получает положительную награду, а при пропуске шарика мимо собственной ракетки - отрицательную. При остальных событиях награды нет. Таким образом, награды очень редкие (точнее в большинстве случаев нулевые).

В игре Atari у противника заложен достаточно простой алгоритм управления ракеткой (который агенту неизвестен). Поэтому это, вообще говоря, среда с неполным описанием. Особенно, если в качестве противника использовать не алгоритм Atari, а другую версию агента.

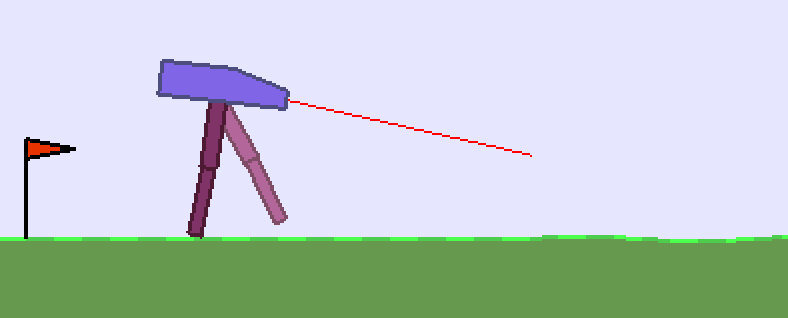
Bipedal Walker

Это одна из задач по управлению механическими моделями роботов. Голова на двух ногах должна научиться перемещаться по слегка пересечённой местности. В каждой ноге есть два шарнира с моторами, которыми управляет агент.

Действие агента состоит из четырёх вещественных чисел (крутящий момент приложенный к двигателям в суставах робота). Наблюдения состоят из 24 вещественных чисел. Первые 14 определяют скорости головы, ног и факт контроля ими поверхности. Ещё 10 компонент вектора наблюдения являются результатами работы ладара (аналог радара, но лазерного). Награды положительные при продвижении робота вперёд и равны -100 при его падании на землю. Активное применение моторов отнимает от наград небольшие величины. Задача - оптимально продвинуться без падений как можно дальше за 1600 временных шагов.

В отличии от предыдущих задач - действия в этой среде непрерывны.

Рекомендательная система

Предположим пользователям в интернете показывается некоторая информация (новость, товар и т.п.). Кроме неё приводятся также краткие описания "сопутствующей" информации (других новостей или товаров). Задача состоит в показе наиболее релевантной сопутствующей информации для данного клиента.

Наблюдением является объединение вектора признаков информации и признаков, характеризующих клиента. Действие - выбор (из очень большого множества) конечного числа элементов (сопутствующей информации). Награда - это факт клика на один из показанных элементов.

Если агент учится в реальных условиях, то очевидно, что среда, с которой он взаимодействует, неполная, стохастическая и нестационарная.

Q и V функции

Пусть политика агента $\pi(a|s)$ фиксирована. Она может быть детеминированной или вероятностной, но предполагается, что при принятии решения агент всегда ей следует. Тогда, находясь в состоянии $s_t$ и сделав действие $a_t$ (и далее продолжает следовать $\pi$), он в будущем получит некоторое накопленное вознаграждение, которое принято диконтировать: $$ R_{t+1} = r_{t+1} + \gamma\, r_{t+2} + \gamma^2\, r_{t+3} + ...~=~r_{t+1} + \gamma\,R_{t+2}. $$ Степень дисконтирования $ \gamma \in [0..1]$ является вещественным гиперпараметром обучения. Если $\gamma = 1$, то $R_{t+1}$ - это просто суммарное будущее вознаграждение. При $\gamma$ меньше 1, мы считаем что будущие доходы менее важны для агента чем ближайшие. По факту это отражает неуверенность в этих доходах (неопределённость будущего). Наконец, параметр $\gamma$ технически позволяет работать с расходящимися бесконечными суммами. Так, если все $r_t=r=\mathrm{const}$, то, в силу того, что $1+\gamma+\gamma^2+...=1/(1-\gamma)$, такая сумма будет равна $R_{t+1}=r/(1-\gamma)$. Обычно $\gamma$ находится в диапазоне от 0.9 до 1.

Будем считать, что агент при выборе очередного действия стремится максимизировать будущее накопленное вознаграждение. Так как, и политика, и среда могут быть вероятностными, необходимо максимизировать среднее значение вознаграждение. Если мы находимся в данном состоянии среды $s$ и предпринимаем действие $a$, то это средние от $R_{t+1}$ (обозначаем угловыми скобками) является условным (условия после вертикальной черты): $$ Q^\pi(s,\,a) = \langle R_{t+1} ~|~ s_t=s,\,a_t=a \rangle_\pi $$ Индекс $\pi$ напоминает, что усреднение по различным траекториям (последовательностям состояний и действий) проводится при фиксированной политике агента $\pi$. Если известна оптимальная $Q^*(s,a)$ по всем возможным политикам, то очевиден и выбор оптимального действия в данном состоянии: $$ Q^*(s,a) = \max_\pi Q^\pi(s,a),~~~~~~~~~~~~~~~a^* = \arg\max_a Q^*(s,a), $$ т.е. из всех возможных политик $\pi$ выбирается та, что при которой $Q$ максимальна. Оптимальное действие $a^*$ такое при котором $Q$ максимальна среди всех возможных действий.

Функция $Q(s,a)$ называется функцией полезности текущего состояния и действия или Q-function. Она играет важную роль во многих методах обучения с подкреплением. Некоторые из них, вместо поиска оптимальной функции политики, строят "оптимальную" функцию полезности, а уже с её помощью находят оптимальную политику.

Если при данной политике $\pi(a_1|s) > \pi(a_2|s)$ и для неё $Q^\pi(s,a_1) < Q^\pi(s,a_2)$ - это означает, что существует более оптимальная политка $\pi'$ в которой $\pi'(a_1|s) > \pi'(a_2|s)$. Динамическое программирование (Dynamic programming, DP) - последовательная оценка политики, т.е. вычисление $Q^\pi(s,a)$, затем улучшение политики: $a=\pi(s)=\arg\max_a Q(s,a)$, снова оценка, и т.д. Если среда марковская, DP сходится к оптимальной политике $\pi^*$.

Аналогично можно говорить о функции полезности состояния при данной политике $\pi$: $$ V^\pi(s)=\langle R_{t+1} ~|~ s_t=s \rangle_\pi. $$ Иногда также вводят функцию преимущества (advantage function): $$ A(s,a) = Q(s,a) - V(s), $$ показывающую на сколько лучше или хуже в состоянии $s$ конкретное действие $a$ по сравнению с выбором действия в соответствии с политикой $\pi(a|s)$. Понятно, что для оптимальных политик и ценностей $A^*(s,a^*)=0$. При этом $A^*(s,a)\le 0$. При неоптимальной политики знак $A(s,a)$ может быть любой.

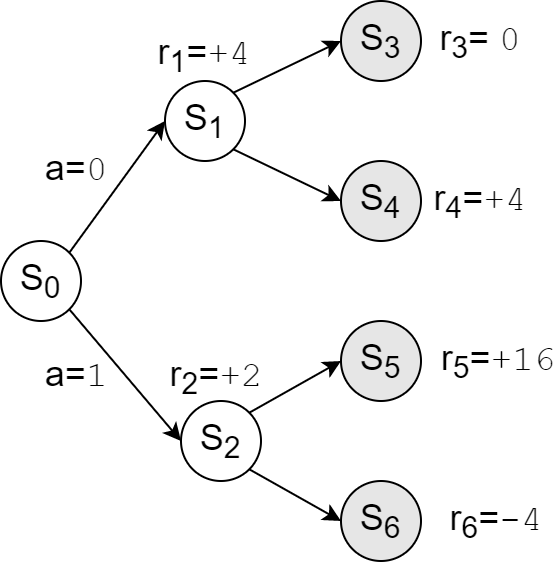
Рассмотрим простой пример, иллюстрирующий приведенные определения. Пусть есть детерминированная среда с семью состояниями, четыре из которых терминальные (серые круги). В каждом состоянии можно сделать одно из двух действий $a\in\{0,1\}$ (вверх или вниз).

Рассмотрим сначала политику при которой агент с равными вероятностями выбирает любое действия в каждом состоянии. В среде возможны четыре равновероятные траектории, начинающиеся с состояния $s_0$. Поэтому ценность состояния $s_0$ равна ($\gamma=1$): $$ V^\pi(s_0)=\frac{1}{4}\,\big[(4+0)+(4+4)+(2+16)+(2-4)\bigr]= \color{red}{\bf 7}. $$ Аналогично вычисляются ценности действий в состоянии $s_0$ (следующая награда плюс средние от дальнейших траекторий): $$ Q^\pi(s_0, 0)=4 + \frac{0+4}{2}=\color{red}{\bf 6},~~~~~~~~~~~~~~~ Q^\pi(s_0, 1)=2 +\frac{16-4}{2}=\color{red}{\bf 8}. $$ Таким образом, функция преимущества $A(s,a)$ для этой политики знакопеременная ($\pm 1$) и действие $a=1$ более "доходно".

Возьмём теперь оптимальную политику которая, очевидно, является детерминированной: $$ \pi^*(s_0) = 1, ~~~~~~~\pi^*(s_1) = 1,~~~~~~~\pi^*(s_2) = 0. $$ Для неё ценности состояния $s_0$ равны: $$ V^*(s_0)=Q^*(s_0,1)= \color{red}{\bf 18},~~~~~~~~Q^*(s_0,0)=\color{red}{\bf 8}. $$ В этом случае теперь $V^*(s)=\max_a Q^*(s,a)$ и $A^*(s_0,0)=-10$, $A^*(s_0,1)=0$. В качечтве упражнения стоит рассмотреть наихудшую политику и вычислить для неё $V$ и $Q$.

Немного математики

Формализуем приведенные выше определения. В дальнейшем эти формулы станут понятнее при их рассмотрении в частных случаях. Пусть $s_t$ - состояние среды в момент времени $t$. Для сред с полным описанием $s_t=o_t$. В общем случае состояние - это некоторая функция текущего наблюдения и всех предыдущих наблюдений и действий $s_t=\{o_0,a_0,...,o_{t-1},a_{t-1},o_{t}\}$. Определим:

Для немарковских процессов в условиях вероятностей $\pi$ и $P$ может стоять не только текущее состояние, но и вся предшествующая история состояний (наблюдений) и действий. Вероятность траектории данного эпизода равна вероятности того, что начальным состоянием будет $s_0$ и в нём агент сделает действие $a_0$, среда перейдёт в состояние $s_1$, выдав награду $r_1$ и т.д., Результат равен произведению этих вероятностей: $$ P^\pi(\tau_0) = p(s_0)\cdot \pi(a_0|s_0)\,P(s_1,r_1| s_{0},a_{0})\cdot\pi(a_1|s_1)\,P(s_2,r_2| s_{1},a_{1})\cdot... $$ Суммарное будущее дисконтированное вознаграждение, начиная с момента времени $t$ равно: $$ R_t = \sum^{\infty}_{i=0} \gamma^{i}\,r_{t+i} = r_t+\gamma\, r_{t+1} + \gamma^2\, r_{t+2}+... ~=~ r_t + \gamma\,R_{t+1}. $$ Общая успешность агента при многократном прохождении эпизодов равна среднему от этой величины по всем возможным траекториям $\tau_0$: $$ R(\pi) = \langle R_1\rangle_\pi = \sum_{s_{0},\,a_0,\,s_1,\,r_1,\,a_1,...} P^\pi(\tau_0)\, R_1. $$ В случае непрерывных наблюдений и/или действий, суммы заменяются на интегралы. Индекс $\pi$ подчёркивает, что среднее вычисляется при фиксированой политике агента $\pi(a|s)$. Из всех возможных политик оптимальной будет политика: $$ \pi^* = \arg\max_\pi R(\pi). $$

Полезность состояния и действия $(s,a)$ при данной политике $\pi$ равна среднему дисконтированному вознаграждению, который агент получит в будущем, совершая в состоянии $s$ действие $a$: $$ Q^\pi(s,a) = \langle R_{t+1} | s_t=s,\,a_t=a \rangle_\pi. $$ Угловые скобки означают среднее по всем последующим состояниям, наградам и действием. Эта условная вероятность равна: $$ Q^\pi(s_t,a_t) = \sum_{s_{t+1},\,a_{t+1},\,r_{t+1},...} \bigr[ P(s_{t+1},r_{t+1}|s_t,a_t)\cdot\pi(a_{t+1}|s_{t+1})\,P(s_{t+2},r_{t+2}|s_{t+1},a_{t+1})\cdot...\bigr]\cdot R_{t+1}. $$ Полезность состояния $s$ при данной политике $\pi$ равна среднему дисконтированному вознаграждению, который агент получит, стартуя из состояния $s$ (индекс $\pi$ далее опускаем): $$ V(s) = \sum_a \pi(a|s)\, Q(s,a). $$ Функция полезности состояния и состояния-действия удовлетворяют уравнениям Беллмана: $$ Q(s,a) = \sum_{s',\,r'} P(s',r'\,|\,s, a)\,\bigr[ r' + \gamma\,V(s')\bigr]. $$ Эти уравнения основаны на соотношении $R_t=r_t+\gamma\,R_{t+1}$. Так, полезность состояния $V(s)$ равна награде в следующем состоянии $s'$ плюс дисконтированная полезность этого состояния (будущие награды из него). Всё это усредняется по всем возможным действиям и состояниям $s'$ : $$ V(s) = \sum_{a,\,s',\,r'} \pi(a|s)\,P(s',r'|s,a)\, \bigr[ r' + \gamma\,V(s') ]. $$ Подробнее эти уравнения обсуждаются в следующем документе.

Классификация методов ML

В машинном обучении с подкреплением разработано множество различных алгоритмов. В отличии от стандартного обучения с учителем, эти методы очень чувствительны к гиперпарамерам и учатся очень долго. Кроме этого, нет универсальных методов. В зависимости от задачи, тот или иной метод может быть неэффективным или вообще не работать. Некоторые методы работают только с дискретными действиями, а другие только с непрерывными.

✒ Сравнивая методы по эффективности, обращают внимание на три основных критерия:

Стоит помнить, что обучение с подкреплением имитирует обучение в реальном мире. Поэтому, оптимальный метод который учится очень долго может оказаться бесполезным в "продакшене", когда его применение и дообучение и совпадают. Интегральным критерием сравнения методов может служить площадь под кривой средней награды в эпизоде как функция числа эпизодов при обучении.

✒ По использованию данных для обучения различат:

Строго говоря, все методы ML являются online-методами, так как если и есть накопление данных, то оно происходит "скользящим окном", с забыванием очень старых. Однако некоторые "сильно онлайновые" методы запускают обучение после каждого временного шага и историю состояний и действий не накапливают. Более офлайновые методы могут сначала пройти один или несколько эпизодов, а потом включить режим обучения. Наконец некоторые методы имеет достаточно большой, но конечный обновляемый буфер памяти, все данные из которого используются при обучении - это уже "сильно офлайновые" методы.

✒ По способу использования политики для оценки качества различают методы:

В off-policy методах обычно существует две политики (или функции из которых получают политику). На основании одной "изучаемой" политике, называемой целевой (target), принимаются решения по выбору действия. Вторая, политика использует эти решения для обучаения. Со временем, обученная политика становится целевой.

✒ По использованию в методе модели, политики, функций ценности различают методы:

Некоторое представление разнообразия методов можно увидеть на следующей диаграмме от OpenAI

Дополнительная информация