ML: Нечёткая логика
Введение
Неопределённость некоторого утверждения может возникать из-за нехватки информации или неопределённости результатов будущих событий. В этих случаях, обычно, используют вероятностную логику. Однако, иногда об утверждении известно всё, но его нельзя считать истинным или ложным. Обычно это оценочные, сравнительные суждения: "Маша красивая" (но всё же не мечта); "Кофе горячий" (но пить его уже можно). Оценочный характер имеют также оппозиционные нечёткие квантификаторы:
Нечётким может быть отношение: $\text{in}(x,y)$ - "объект $x$ находится внутри объекта $y$". Например, "карандаш в пенале" может немного выглядывать из пенала, тем не менее находясь внутри него.
Наконец, нечёткими могут быть правила:
Логические связки
Будем считать, что оценочное суждение $A$ характеризуется степенью истинности $T_A$, которое является вещественным числом из диапазона $[0...1]$. Значение $T_A=0$ соответствует ложному суждению, а $T_A =1$ - истинному. Промежуточные значения - это "промежуточная истинность". При, например, $T_A=0.7$ для $A:$ "Маша красивая", означает, что утверждение скорее истинно, чем ложно.
Степень истинности логического отрицания "НЕ $A$" естественно определить следующим образом:$$ \neg A:~~1-T_A. $$
Для логических И, ИЛИ чаще всего используются минимум и максимум степеней истинности суждений: $$ A\,\&\,B:~~~\min(T_A,T_B),~~~~~~~~~~~~~A\vee B:~~~\max(T_A,T_B). $$ Напомним, что в теории вероятности неравенства $P(A\,\&\,B)\le \min(P_A,\,P_B)$ и $ \max(P_A,\,P_B)\le P(A\vee B)$ выполняются для любых двух событий. Нечёткая логика не эквивалентна теории вероятностей или вероятностной логике и использует верхнюю границу для конъюнкции ($\,\&\,$) и нижнюю для дизъюнкции ($\vee $).
Ниже на рисунках приведены карты высот для степеней истинности результатов логических операций:
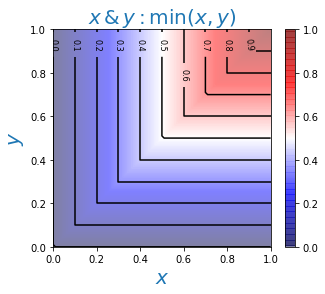
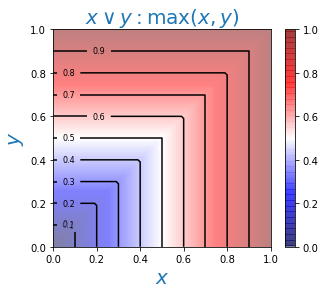
Таким образом определённые логические связки удовлетворяют всем аксиомам булевой алгебры, за исключением закона исключения третьего: $$ A\vee \neg A = 1,~~~~~~~~~~~~~~~A\,\&\,\neg A = 0. $$ Стоит это проверить, например, для $T_A=0.5$. Нарушение этого закона типично для многозначных логик, в которых требование, чтобы утверждение было или истинным, или ложным уже, очевидно, теряет свой смысл.
Отметим, что в вероятностной логике степень истинности $P(A\,\&\,B)$ зависит не только от $P(A)$ и $P(B)$, но и от степени скоррелированности (зависимости) этих утверждений (событий). В нечёткой логике подобная корреляция игнорируется.
В дальнейшем, если это не будет приводить к неоднозначности, вместо $T_A$ будем просто писать $A$. Тогда для отрицания $\neg A=1-A$, дизъюнкции $A\vee B =\max(A,B)$ и конъюнкции $A\,\&\, B =\min(A,B)$.
Нечёткие множества
Истинность оценочных суждений удобно описывать при помощи еории множеств. Говоря о том, что "Маша красивая", мы подразумеваем множество красивых женщин, к которому с той или иной степенью точности принадлежит Маша.
Таким образом, в теории нечётких множеств вводится функция принадлежности $\mu_A(x)$, характеризующая степень принадлежности объекта $x$ к множеству $A$: $x\in A$. Значения этой функции лежат в интервале $[0...1]$, где $1$ означает точно принадлежит, а $0$ - точно не принадлежит.
 Объединение $A\cup B$ нечётких множеств $A$, $B$
соответствует дизъюнкции (ИЛИ), а пересечение $A\cap B$ - конъюнкции (И).
Поэтому их функции принадлежности равны:
$$
\begin{array}{lll}
\mu_{A\cap B}(x) = \min\{ \mu_A(x),~\mu_B(x)\},\\
\mu_{A\cup B}(x) = \max\{ \mu_A(x),~\mu_B(x)\}.
\end{array}
$$
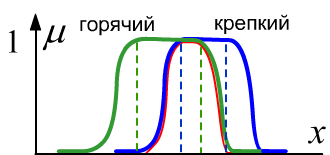
Справа на рисунке в виде прямой $x$
изображено множество различных чашек с кофе (эти объекты не упорядочены и обычно рисуются
областями на плоскости). Каждой чашке соответствует то или иное значение её принадлежности к
множествам "горячий" и "крепкий".
Пунктиры - это границы чётких множеств. Красная линия является функцией принадлежности
пересечения множеств ($\min$).
Объединение $A\cup B$ нечётких множеств $A$, $B$
соответствует дизъюнкции (ИЛИ), а пересечение $A\cap B$ - конъюнкции (И).
Поэтому их функции принадлежности равны:
$$
\begin{array}{lll}
\mu_{A\cap B}(x) = \min\{ \mu_A(x),~\mu_B(x)\},\\
\mu_{A\cup B}(x) = \max\{ \mu_A(x),~\mu_B(x)\}.
\end{array}
$$
Справа на рисунке в виде прямой $x$
изображено множество различных чашек с кофе (эти объекты не упорядочены и обычно рисуются
областями на плоскости). Каждой чашке соответствует то или иное значение её принадлежности к
множествам "горячий" и "крепкий".
Пунктиры - это границы чётких множеств. Красная линия является функцией принадлежности
пересечения множеств ($\min$).
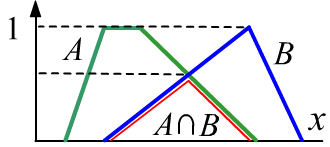 В этом примере нечёткое пересечение включает чёткое пересечение,
т.к. его высота (максимальное значение) равна 1.
Но в общем случае это может быть и не так (если высота меньше 1).
Множество называется нормальным, если его высота равна 1.
Справа приведен пример в котором перечечение не является нормальным.
В этом примере нечёткое пересечение включает чёткое пересечение,
т.к. его высота (максимальное значение) равна 1.
Но в общем случае это может быть и не так (если высота меньше 1).
Множество называется нормальным, если его высота равна 1.
Справа приведен пример в котором перечечение не является нормальным.
Включение или строгое подмножество $A\subset B$ по определению истинно, если $\mu_A(x) \lt \mu_B(x)$. В противном случае оно ложно. Это чёткое логическое понятие. Различными способами можно определить и нечёткое включение (например, как нормированную сумму $|\mu_A(x)-\mu_B(x)|$ по всем элементам множества $x$).
Срезом нечёткого множества $A$ на уровне $\alpha$ называется множество элементов для которых функция принадлежности больше уровня: $\{x|~ \mu_A(x) \ge \alpha\}$. Эти элементы принадлежат $A$ с точностью не менее $\alpha$.
Логическое высказывание "кофе горячий и крепкий" означает, что существует множество различных чашек кофе. Часть из них относится к множеству "горячий", а часть к множеству "крепкий". Данная чашка (о которой идёт речь в утверждении) принадлежит к обоим множествам (в нечётком смысле).
Нечёткие предикаты
В бинарной логике высказывания являются частным случаем предикатов. Предикат является логической функцией (значения $0,1$) предметных переменных: $A(x),~ B(x,y)$. Предметные переменные - это элементы некоторых множеств (области определения предиката). Примеры предикатов: $P(x)$ - число $x$ положительно, $M(x,y)$ - некая $x$ является матерью для $y$, $A \in \alpha$ - точка $A$ лежит на прямой $\alpha$.
В нечёткой логике значения предикатов, естественно, лежат в диапазоне $[0...1]$. Унарные предикаты $A(x)$ являются нечёткими функциями приндлежности элемента $x$ множеству $A$. Выше для $x\in A$ мы использовали a $\mu_A(x)$, теперь для краткости будем писать просто $A(x)$.
Частными случаями нечётких предикатов являются нечеткие переменные и отношения.
Нечёткие переменные
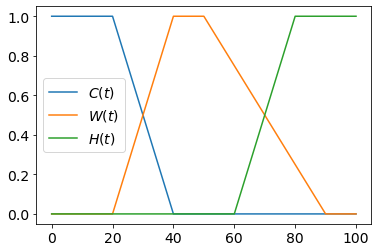 Нечёткая переменная - это предикат, зависящий от одного или нескольких вещественных чисел..
Например, говоря о кофе, можно определить следующие
нечёткие переменные, зависящие от его температуры $t$:
Нечёткая переменная - это предикат, зависящий от одного или нескольких вещественных чисел..
Например, говоря о кофе, можно определить следующие
нечёткие переменные, зависящие от его температуры $t$:
Другие примеры: медленный, быстрый (функции скорости); лёгкий, тяжёлый (функции массы); молодой, старый (функции возраста) и т.д.
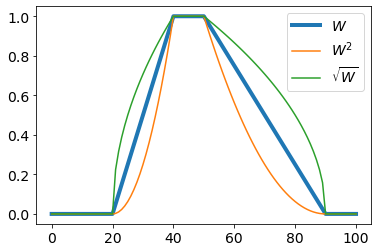 К нечётким переменным можно применять различные модификаторы:
$$
\text{очень}:~~~~A^2(x),~~~~~~\text{не очень}:~~~~\sqrt{A(x)}.
$$
Так "очень тёплый"
$W^2(t)$ усиливает функцию $W(t)$, а "не очень тёплый" $\sqrt{W(t)}$ её ослабляет.
Первый модификатор называют также концентрацией,
а второй - разбавлением.
К нечётким переменным можно применять различные модификаторы:
$$
\text{очень}:~~~~A^2(x),~~~~~~\text{не очень}:~~~~\sqrt{A(x)}.
$$
Так "очень тёплый"
$W^2(t)$ усиливает функцию $W(t)$, а "не очень тёплый" $\sqrt{W(t)}$ её ослабляет.
Первый модификатор называют также концентрацией,
а второй - разбавлением.
Приведём пример формирования трапецивидной функции принадлежности, зависящей от одной вещественной переменной, на Python при помощи библиотеки NumPy:
def tra(min_X, x1,x2,x3,x4, max_X, num=100):
X = np.linspace(min_X, max_X, num, dtype = 'float32')
Y = np.zeros_like(X)
idx = (X >= x1) & (X <= x2); Y[idx] = (X[idx]-x1)/(x2-x1)
idx = (X > x2) & (X <= x3); Y[idx] = 1
idx = (X > x3) & (X <= x4); Y[idx] = (x4-X[idx])/(x4-x3)
return X,Y
Нечёткие отношения
Нечёткое отношение является предикатом, зависящим от двух предметных переменных. Функция $R(x,y)$ данной паре сущностей $x,y$ (предметных констант) ставит в соответствие вещественное число из диапазона $[0...1]$ (степень истинности отношения). Например, для отношения "два числа почти совпадают" $x\approx y$ можно положить $R(x,y)=e^{-(x-y)^2}.$ Тогда $R(x,x)=1$; если $x$ и $y$ близки, то $R(x,x)\approx 1$; и в противном случае $R(x,y)\to 0$.
В бинарной логике отношение $R(x,y)$ является подмножеством множества пар (декартово произведение) $\mathbb{X}\times \mathbb{Y}$. Поэтому нечёткое отношение является нечётким множеством. Все определения (объединение, пересечение, дополнение отношений и т.д.) на этот случай переносятся без изменений.
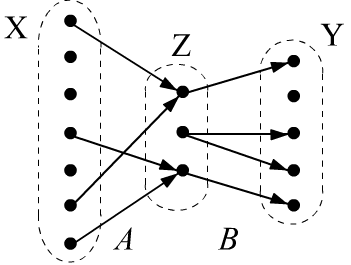 Рассмотрим подробнее композицию $(A \circ B)(x,y)$ двух отношений $A(x,z)$ и $B(z,y)$.
Рассмотрим подробнее композицию $(A \circ B)(x,y)$ двух отношений $A(x,z)$ и $B(z,y)$.
Пусть есть три множества $\mathbb{X},\mathbb{Z},\mathbb{Y}$ (в общем случае различные).
Отношение $A(x,z)$ задано на множестве $\mathbb{X}\times \mathbb{Z}$,
а отношение $B(z,y)$ на множестве $\mathbb{Z}\times \mathbb{Y}$.
В бинарной логике, если $A(x_i,z_k)$ истинно, то элементы $x_i$ и $z_k$ связаны отношением $A$.
Это можно представить в виде стрелки из $x_i$ в $z_k$ (см. рисунок справа).
Композиция отношений $(A \circ B)(x_i,y_j)$ будет истинна,
если из $x_i$ можно "попасть" в $y_j$ через некоторый $z_k$. Формально это записывается
при помощи квантора существования (есть такой $z$, что ...):
$$
(A \circ B)(x,y) : ~~~~~~\exists_z\, A(x,z)\,\&\,B(z,y) = \bigr[A(x,z_1)\,\&\,B(z_1,y)\bigr]\vee \bigr[A(x,z_2)\,\&\,B(z_2,y)\bigr]\vee ...,
$$
где квантор существования выражен через "сумму" логических ИЛИ по всем элементам конечного множества $\mathbb{Z}$.
Для нечётких отношений это определение обобщается естественным образом:
$$
(A \circ B)(x,y) = \max_z \bigr[\min\{A(x,z),~B(z,y)\}\bigr],
$$
где для $\max$ вычисляется по всем элементам $z\in \mathbb{Z}$.
Часто встречаются следующие аксиомы фиксирующие свойства отношений: $$ \begin{array}{lllll} \text{рефлексивное} & R(x,x) = 1 \\ \text{антирефлексивное} & R(x,x) = 0 \\ \text{симметричное} & R(x,y) = R(y,x) \\ \text{асимметричное} & \min\bigr\{R(x,y),\,R(y,x)\bigr\} = 0 \\ \text{антисимметричное} & x\neq y ~\Rightarrow~ \min\bigr\{R(x,y),\,R(y,x)\bigr\} = 0 \\ \text{транзитивное} & \min\bigr\{R(x,y),\,R(y,z)\bigr\} \le R(x,z) \\ \end{array} $$ Например, отношение близости $x\approx y$ рефлексивно и симметрично.
Норма и конорма *
Выбор функций $\min$ для конъюнкции (пересечения) и $\max$ для дизъюнкции (объединения) не является единственно возможным (хотя часто он более предпочтителен). Обозначим логическое И в виде функции $T(x,y)$ (норма), а логическое $ИЛИ$ как $S(x,y)$ (конорма). Потребуем, чтобы они были симметричными и ассоциативными: $$ \begin{array}{llll} \&:~ \\ \vee\,:\\ \end{array}~~~~~~~~~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} T(x,y) &=& T(y,x) \\ S(x,y) &=& S(y,x) \end{array}\right.,~~~~~~~~~~~~~~~~~~~ \left\{ \begin{array}{lcl} T(x, T(y,z)) &=& T(T(x, y),z)\\ S(x, S(y,z)) &=& S(S(x, y),z)\\ \end{array}\right.. $$ Кроме этого наложим свойства ограниченности и монотонности (выполняющиеся для $\&, \vee$ и в бинарной логике): $$ \begin{array}{llll} \&:~ \\ \vee\,:\\ \end{array}~~~~~ \left\{ \begin{array}{llll} T(0,0) = 0, & T(1,x) = x\\ S(1,1) = 1, & S(0,x) = x\\ \end{array} \right.,~~~~~~~ \left\{ \begin{array}{llll} x_1 \le x_2,~~~ y_1 \le y_2~~~\Rightarrow~~~~~T(x_1, y_1) \le T(x_2, y_2)\\ x_1 \ge x_2,~~~ y_1 \ge y_2~~~\Rightarrow~~~~~S(x_1, y_1) \ge S(x_2, y_2)\\ \end{array} \right.. $$Отметим, что условие монотонности выполняется не только в булевой логике, но и достаточно естественно для нечёткой логики. Например: $0.5 \,\&\, 0.8 ~\lt~ 0.7 \,\&\, 0.9$ означет, что $0.5$ менее истинно, чем $0.7~~~$ И $~~~0.8$ менее истинно, чем $0.9$.
Будем также предполагать, что выполняются законы де-Моргана $\neg(X\,\&\,Y) = \neg X\vee \neg Y$ и $\neg(X\vee Y) = \neg X\,\&\, \neg Y$, связывающие эти две операции: $$ \begin{array}{llll} 1-T(x,y) = S(1-x,1-y), & ~~~~~ & 1-S(x,y) = T(1-x,1-y). \\ \end{array} $$ Возможны различные функции, удовлетворяющие этим аксиомам (обычно задаётся, например, $T(x,y)$, а $S(x,y)$ получается из закона де-Моргана). Приведём для примера три следующих варианта: $$ \begin{array}{l|c|c|l|l|} & \text{1. логические} & \text{2. алгебраические} & \text{3.} \\ \hline A\,\&\,B & \min(A,B) & A\,B & \max(A+B-1,~ 0) \\ A\vee B & \max(A,B) & A+B - A\,B & \min(A+B,~ 1) \\ \hline A \,\&\, A \equiv A & \mathbb{T} & (0,1) & (0, 1) \\ A \vee A \equiv A & \mathbb{T} & (0,1) & (0, 1) \\ A \,\&\, \neg A & (0.0,0.5) & (0,0.25) & \mathbb{F} \\ A \vee \neg A & (0.5,1.0) & (0.75,1) & \mathbb{T} \\ A\,\&\,(B\vee C) \equiv~... & \mathbb{T} & (0,1) & (0, 1) \\ A\vee (B\,\&\,C)\equiv~... & \mathbb{T} & (0,1) & (0, 1) \\ \end{array} $$ Под определением связок указаны значения истинности некоторых тождеств булевой алгебры при использовании этих связок. Если стоит $\mathbb{T}$ - тождество истинно, при $\mathbb{F}$ - ложно, в противном случае указаны диапазоны изменения истинности при всех возможных значениях истинности аргументов.
Обратим внимание, что законы исключения третьего для варианта (3.) выполняются, а в остальных случаях $A \,\&\, \neg A$ стремиться быть скорее ложным, а $A \vee \neg A$ - скорее истинным. Свойства идемпотентности: $$ A\,\&\,A \equiv A,~~~~~~~~~~~~A\vee A \equiv A. $$ выполняются только для "логического" варианта ($\min,\max$). На самом деле, это очень естественные свойства, как для логических величин, так и для множеств ($A\cap A=A$ и $A\cup A=A$). Поэтому, обычно, их выполнение желательно.
Отметим также, что для определений 2,3 нарушаются законы дистрибутивности: $$ \begin{array}{lcl} A\,\&\,(B\vee C) &\equiv& (A\,\&\,B)\vee (A\,\&\,B)\\ A\vee(B\,\&\,C) &\equiv& (A\vee B)\,\&\, (A\vee B). \end{array} $$ Это не так критично, но не вполне соответствует обыденному пониманию смысла логических операций.
Импликация
В булевой логике важную роль играет импликация: $A\to B$. Эта логическая связка в языке соответствует фразам: "из $A$ следует $B$", "если $A$, то $B$". Принято, что она ложна только для $1\to 0$ ("из истины нельзя получить ложь"). Во всех остальных случаях: $0\to 0$, $0\to 1$, $1\to 1$ она истинна.
Обычно предполагается наличие некоторой связи между посылкой $A$ и следствием $B$ импликации $A\to B$.
Так, в арифметике при любом $x$ истинна формула: $(x<2) \to (x<4)$.
Когда посылка истинна ($x=1$), истинно и следствие.
Если же посылка ложна, то следствие может быть как истинным (при $x=3$),
так и ложным ($x=5$).
"Менее правильное" утверждение $(x > 2) \to (x < 4)$ ложно при $x=5$.
В нечёткой логике нет единого мнения какое выражение следует использовать для импликации . Ниже приведены некоторые варианты, предлагавшиеся различными авторами:
$$ A\to B:~~~~~~~~~~~~~~~~~~~ \begin{array}{lll} \text{Клини} & \neg A \vee B & ~~~~~ & \max(1-A,~B) \\ \text{Заде} & \neg A \vee (A\,\&\,B)& & \max(1-A,~\min(A,B)) \\ \text{Вади} & & & \max(1-A, ~A\,B)\\ \\ \text{Шарп} & & & \text{if}(A \le B)~ \{1,~0\} \\ \text{Брауэр} & & & \text{if}(A \le B)~ \{1,~B\} \\ \text{Лукасевич} & & & \text{if}(A \le B)~ \{1,~B+1-A\} \\ \text{Гоген} & & & \text{if}(A \le B)~ \{1,~B/A\}, \\ \end{array} $$где конструкция $\text{if}(C)\{A, B\}$ равна $A$, если $C$ истинно и $B$ в противном случае. Все эти определения воспроизводят булеву импликацию для значений $0,1$.

Первые три определения "крутятся" вокруг выражения импликации через диъюнкцию в бинарной логике. В определении Клини это записано в явном виде. У Заде, при выполнении дистрибутивности (для $\&=\min,$ $\vee=\max$), можно записать $(\neg A \vee A)\,\&\,(\neg A \vee B)$. Первая скобка в бинарной логике равна $1$. В нечёткой (с $\min$, $\max$) она больше $0.5$ и тем ближе к $1$, чем истиннее $A$. Численные значения этих импликаций отличаются, если один из аргументов связки находится в окрестности неопределённого значения $0.5$.
Последние четыре опредления исходят из того, что импликация должна быть строго истинной, если из менее истинного утверждения "следует" не менее истинное ($A \le B$). Отличия возникают когда $A$ истиннее $B$.
Логический вывод
 В бинарной логике из $P$ логически следует $Q$,
если всегда, когда формула $P$ истинна, то истинна и формула $Q$.
Это обозначается так: $P\Rightarrow Q$.
Логический вывод - это способ получения одних истинных формул из других, также истинных.
Не стоит путать вывод и импликацию $P\to Q$, которая является логической связкой,
принимающая значения $0$ или $1$.
В бинарной логике из $P$ логически следует $Q$,
если всегда, когда формула $P$ истинна, то истинна и формула $Q$.
Это обозначается так: $P\Rightarrow Q$.
Логический вывод - это способ получения одних истинных формул из других, также истинных.
Не стоит путать вывод и импликацию $P\to Q$, которая является логической связкой,
принимающая значения $0$ или $1$.
Рассмотрим простейший пример логического вывода: если истинна конъюнкция утверждений, то истинно (выводимо) каждое из утверждений. В нечёткой логике это правило обобщается очевидным образом, приводя к интервальным оценкам для выводимой формулы: $$ A\,\&\,B~~~~~ \Rightarrow~~~~~~ A,~~~~~~~~~~~~~~~~~~~~~~\min(A,~B) ~~~\le~~~ A ~~~\le~~~ 1, $$ где $\min(A,~B)$, с одной стороны является значением конъюнкции $A\,\&\,B$, а с другой, нижней границей для $A$. Естественно, в данном выводе предполагается, что степень истинности $A\,\&\,B$ задана и в результате логического вывода, она ограничивает снизу значение истинности $A$. Аналогично интерпретируются неравенства для следующего вывода: $$ A~~~~~ \Rightarrow~~~~~~ A\vee B,~~~~~~~~~~~~~~~~~~~~~~0 ~~~\le~~~ A ~~~\le~~~ \max(A,~B). $$
Таким образом, в нечёткой логике, по-мимо указания выводимой формулы, необходимо уметь вычислять степень её истинности. Определение такого логического вывода не вполне неоднозначно, что отражено в многообразии предложенных вариантов для импликации двух высказываний.
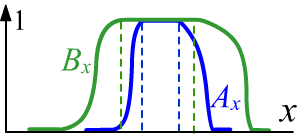 Одна из возможностей, как и в вероятностной логике
считать, что $A~\Rightarrow~B$, если $A \le B$.
Примеры выводов, приведенные выше, удовлетворяют этому условию.
В случае предикатов, заданных на одном множестве
$\mathbb{X}$, такой вывод $A(x)~\Rightarrow~B(x)$ означает, что $A\subset B$ и множества $A,B$
являются нормальными, т.е. имеют единичную высоту (см. рисунок справа).
Тогда на срезе $\alpha=1$, $A$ будет обычным подмножеством $B$.
Одна из возможностей, как и в вероятностной логике
считать, что $A~\Rightarrow~B$, если $A \le B$.
Примеры выводов, приведенные выше, удовлетворяют этому условию.
В случае предикатов, заданных на одном множестве
$\mathbb{X}$, такой вывод $A(x)~\Rightarrow~B(x)$ означает, что $A\subset B$ и множества $A,B$
являются нормальными, т.е. имеют единичную высоту (см. рисунок справа).
Тогда на срезе $\alpha=1$, $A$ будет обычным подмножеством $B$.
Часто знания (обыденные или математические) формулируют как правила "ЕСЛИ ... TO ..."
(импликация).
Тогда в бинарной логике
важными методами вывода являются modus ponens и modus tollens
(запись посылок вывода через запятую подразумевает
связывание их логическим И):
$$
\begin{array}{cccccc}
A, & A\to B&~~~~~~~~&\Rightarrow&~~~~~~~~&B\\
\neg B,& A\to B&~~~~~~~~&\Rightarrow&~~~~~~~~&\neg A\\
\end{array}
$$
Считая эти выводы справедливыми в нечёткой логике,
найдём значения истинности получаемых формул.
Для modus ponens имеем $\min(A,~A\to B) ~\le~ B~\le~ 1$. В случае когда "аксиома" $A \to B$ всегда истинна, то $A \le B$. Если $A=1$, то $B=1$ (бинарный случай), а при $A=0$ имеем $0 \le B\le 1$, т.е. значение $B$ полностью не определено (что также согласуется с бинарной логикой). Для modus tollens для истинного правила $A \to B$ также получаем $$ A ~\le~ B ~\le~ 1. $$ Напомним, что получение значение истинности выводимых формул в виде неравенства типично и для вероятностной логики.
Когда истинность правила $A\to B$ отлична от $1$, необходим выбор той или иной формулы для импликации. Отметим также, что из всех определений импликации с неравенством $\min(A,~A\to B) \le B$ в общем случае согласуются только импликации Шарпа и Брауэра.
Рассмотрим простой пример из двух правил: $$ A\to B,~~~~~~~\neg A\to \neg B. $$ Например, они справедливы для $A$: "сильно ударить по стеклу", $B$: "стекло разобьётся". Из первого правила следует, что $A \le B$, а из второго $1-A \le 1-B$ или $B\le A$. Поэтому $B = A$ (точное значение при заданном $A$). Это естественный результат: если по стеклу ударить несильно ($A = 0.2$), то видимо оно не разобьётся ($B = 0.2$).
✒ В бинарной логике существует очень мощный метод вывода по резолюции, применяемый в машинном выводе: $$ A\vee C,~\neg A\vee B~~~~~~~~~~\Rightarrow~~~~~~~~~~C\vee B. $$ В нечёткой логике он не работает, т.к. неравенство $\min\bigr(\max(A,C),~\max(1-A, B)\,\bigr)~\le \max(C,B)$ не является верным (например, для $A=1/2,~B=C=0$). Это связано с нарушением закона исключения третьего. В бинарной логике резолюция означает, если посылки истинны, то либо $A=0$ и тогда $C=1$, $B$ - любое, либо $A=1$ и тогда $B=1$, $C$ - любое. Поэтому в любом случае $B \vee C$ истинно.
Вывод Заде для предикатов
Вывод Заде обобщает правило modus ponens на случай нечётких предикатов. Пусть есть правило $A(x)\to B(y)$ и задан предикат $A'(x)$ "похожий" на $A(x)$. Тогда: $$ A'(x),~~A(x)\to B(y)~~~~~~~~~\Rightarrow~~~~~~~B'(x) = A'\circ (A\to B) = \max_x\bigr[ \min\bigr[ A'(x),~ A(x)\to B(y)\bigr]\bigr]. $$ Нечёткое правило $A(x)\to B(y)$ может быть задано в виде отношения (матрица $\mathbb{X}\times\mathbb{Y}$) или вычислено при помощи заданных предикатов $A(x), B(y)$ и одного из определений импликации (что проще).
В частном случае высказываний $A'=A$ и импликации Брауэра $A\to B:~R=\text{ if }(A \le B): \{~1;~ B\}$, получаем: $$ B' = \left\{ \begin{array}{llll} \min(A,~1)=A, & ~~~& A \le B \\ \min(A,~B)=B, & ~~~& A \gt B \end{array} \right. ~~~~~=~~~~ \min(A,B) $$ Если $A=1$, то $B'= B = R$ (степени истинности правила), если $A=0$, то $B'=0$ (?), хотя в бинарной логике истинность $B$ не определена. При $A=0.5$ имеем $B'=0.5$.
Вывод Мамдани
Логический вывод Мамдани - это эвристический способ нечётких рассуждений, который используется при наличии набора правил, содержащих нечёткие переменные. Пусть, например, есть два правила, зависящие от 6 нечётких переменных $A_i,B_i,C_i$, определяемых тремя параметрами $x,y,z$: $$ \begin{array}{llll} A_1(x) \,\&\,B_1(y) \to C_1(z),\\ A_2(x) \,\&\,B_2(y) \to C_2(z).\\ \end{array} $$ Предположим, что значения вещественных параметров $x,y$ известны и равны $x_0,y_0$.Задача состоит в определении наиболее подходящего значения параметра $z$, удовлетворяющего этим правилам.
На первом этапе поиска $z$ проводится фаззификация (получение значений
нечётких переменных $A_1(x_0)$ и т.д.)
и вычисление значений посылок на основе формул нечёткой логики ($\min$ для $\&$ и $\max$ для $\vee$):
$$
\left\{
\begin{array}{llll}
\alpha_1 = \min\bigr(A_1(x_0),~B_1(y_0)\bigr) \\
\alpha_2 = \min\bigr(A_2(x_0),~B_2(y_0)\bigr)
\end{array}\right.,
~~~~~~~~~~~~~~
\left\{
\begin{array}{llll}
\alpha_1 \to C_1(z)\\
\alpha_2 \to C_2(z)\\
\end{array}\right..
$$
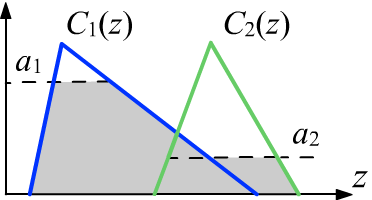 Затем "активизируются" следствия правил, в предположении,
что их истинность не должна превышать истинности посылок (справа на рисунке уровни $\alpha_i$
отсекают более высокие значения истинности следствий):
$$
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~C'_i(z) = \min (\alpha_i, C(z)).
$$
Эти модифицированные следствия объединяются
по всем правилам (логическое ИЛИ), в результате чего
получается функция распределения $\mu(z)\in[0...1]$ для переменной $z$:
$$
\mu(z) = \max_i C'_i(z).~~~~~~
$$
На последнем этапе проводится дефаззификация, в результате которой
выбирается конкретное значение для $z$.
Например, можно взять
точку центра тяжести функции $\mu(z)$:
$$
z_0 =\int z\,\mu(z)\,dz ~\Bigr/~ \int \mu(z)\,dz.
$$
Обратим внимание, что, как на этапе активизации, так и при дефаззификации
посылки с низкой истинностью дают слабый вклад в результат
(совсем ложные посылки вообще на него не влияют).
Поэтому при активизации вместо функции $\min$ можно также
использовать произведение: $C'_i(z)=\alpha_i\,C_i(z)$ (алгоритм Ларсена).
Затем "активизируются" следствия правил, в предположении,
что их истинность не должна превышать истинности посылок (справа на рисунке уровни $\alpha_i$
отсекают более высокие значения истинности следствий):
$$
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~C'_i(z) = \min (\alpha_i, C(z)).
$$
Эти модифицированные следствия объединяются
по всем правилам (логическое ИЛИ), в результате чего
получается функция распределения $\mu(z)\in[0...1]$ для переменной $z$:
$$
\mu(z) = \max_i C'_i(z).~~~~~~
$$
На последнем этапе проводится дефаззификация, в результате которой
выбирается конкретное значение для $z$.
Например, можно взять
точку центра тяжести функции $\mu(z)$:
$$
z_0 =\int z\,\mu(z)\,dz ~\Bigr/~ \int \mu(z)\,dz.
$$
Обратим внимание, что, как на этапе активизации, так и при дефаззификации
посылки с низкой истинностью дают слабый вклад в результат
(совсем ложные посылки вообще на него не влияют).
Поэтому при активизации вместо функции $\min$ можно также
использовать произведение: $C'_i(z)=\alpha_i\,C_i(z)$ (алгоритм Ларсена).
Существует модификация этого метода - вывод Цукамото. На этапе активизации следствий решаются уравнения: $C_i(z) = \alpha_i$, дающие единственные решения $z_i$. Такой подход возможен только, когда нечёткие переменные $C_i(z)$ в правилах являются монотонными функциями $z$ (растущими или убывающими), иначе решений будет несколько. На этапе дефаззификации также вычисляется центр тяжести по полученным решениям $z_1,z_2,...$: $$ z= \sum_i \alpha_i z_i~\Bigr/~\sum_i\alpha_i. $$
Существует также подход Сугено, в котором в правилах следствия записываются в виде инструкций для значений $z=F(x,y)$, где $F$ - некоторые функции (обычно линейные). После фаззификации мы сразу получаем значения $z_i$, по которым, как и выше, при помощи истинностей посылок $\alpha_i$ вычисляется центр тяжести.
Нечёткие числа
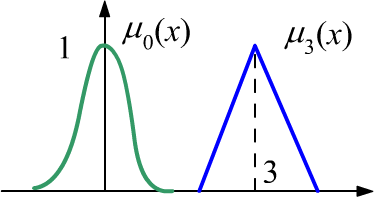 Нечёткое число $X$ - это функция принадлежности $\mu_X(x)$ от вещественного числа $x$,
имеющая единственный единичный максимум при $x=X$. На рисунке справа $\mu_0(x)$ -
это "примерно ноль", а $\mu_3(x)$ - примерно три.
Нечёткое число $X$ - это функция принадлежности $\mu_X(x)$ от вещественного числа $x$,
имеющая единственный единичный максимум при $x=X$. На рисунке справа $\mu_0(x)$ -
это "примерно ноль", а $\mu_3(x)$ - примерно три.
Пусть есть вещественная функция двух (обычных) чисел $z=f(x,y)$ и два нечётких числа $A(x), B(y)$. Нас интересует функция принадлежности $\mu_{f(A,B)}(z)$, равная степени уверенности в том, что конкретное число $z$ является результатом операции (функции) $f$.
Переберём все возможные значения $x,y$ для которых $z=f(x,y)$ и выясним степени уверенности того, что это нечёткие числа $A(x), B(y)$. Тогда по принципу расширения Заде функция принадлежности операции, по определению, будет равна: $$ \mu_{f(A,B)}(z) = \sup_{x,y: f(x,y)=z}\min\bigr\{\mu_A(x),\,\mu_B(y)\bigr\}. $$ Таким образом, из всех возможных "чётких" способов получить $z$ выбираем то, которое даёт наибольшее ($\sup$) значение минимума функций принадлежности нечётких чисел аргументов функции.
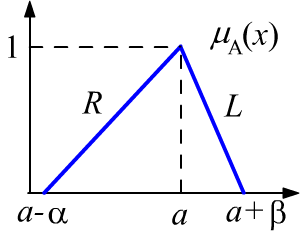 Часто для нечётких чисел используют функции принадлежности $L-R$ типа
$$
\mu_A(x) =
\left\{
\begin{array}{lll}
L(a-x) & x \ge a \\
R(x-a) & x \ge a \\
\end{array}
\right.
~~~~~~~
\begin{array}{lll}
L(0)=R(0) = 1 \\
L,R \text{ - не возрастают} \\
\end{array}
$$
Простейшим примером является треугольная функция принадлежности $\langle a;\, \alpha, \beta \rangle$, приведенная на рисунке.
При помощи принципа расширения для треугольных чисел
можно получить следующие результаты для стандартных арифметических операций:
$$
\begin{array}{lll}
\langle a_1;\, \alpha_1,\beta_1 \rangle \pm \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\pm a_2;\, \alpha_1+\alpha_2,\beta_1+\beta_2 \rangle\\
\langle a_1;\, \alpha_1,\beta_1 \rangle \cdot \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\cdot a_2;\, \alpha_1 a_2+\alpha_2 a_1,\beta_1 b_2+\beta_2 b_1\rangle\\
\langle a;\, \alpha,\beta \rangle^{-1} = \langle 1/a;\, \beta/a^2,\alpha/a^2 \rangle \\
\end{array}
$$
Обратм внимание, что для положения максимума выполняются обычные арифметические операции,
а величина нечёткости (ширина треугольника) увеличивается.
Часто для нечётких чисел используют функции принадлежности $L-R$ типа
$$
\mu_A(x) =
\left\{
\begin{array}{lll}
L(a-x) & x \ge a \\
R(x-a) & x \ge a \\
\end{array}
\right.
~~~~~~~
\begin{array}{lll}
L(0)=R(0) = 1 \\
L,R \text{ - не возрастают} \\
\end{array}
$$
Простейшим примером является треугольная функция принадлежности $\langle a;\, \alpha, \beta \rangle$, приведенная на рисунке.
При помощи принципа расширения для треугольных чисел
можно получить следующие результаты для стандартных арифметических операций:
$$
\begin{array}{lll}
\langle a_1;\, \alpha_1,\beta_1 \rangle \pm \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\pm a_2;\, \alpha_1+\alpha_2,\beta_1+\beta_2 \rangle\\
\langle a_1;\, \alpha_1,\beta_1 \rangle \cdot \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\cdot a_2;\, \alpha_1 a_2+\alpha_2 a_1,\beta_1 b_2+\beta_2 b_1\rangle\\
\langle a;\, \alpha,\beta \rangle^{-1} = \langle 1/a;\, \beta/a^2,\alpha/a^2 \rangle \\
\end{array}
$$
Обратм внимание, что для положения максимума выполняются обычные арифметические операции,
а величина нечёткости (ширина треугольника) увеличивается.
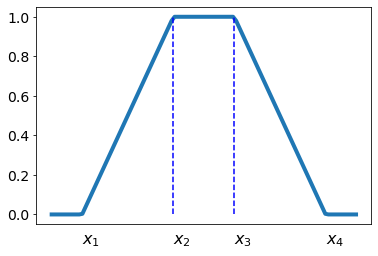
Другой способ задания функций принадлежности $\langle a,b; \alpha, \beta \rangle$ - это трапеция c максимумом на интервале $[a,b]$ и граничными точками $\alpha,\beta$.
Нечёткая логика на Python
Определим класс с перегруженными логическими операторами для нечёткой логики:
class Fuzzy:
def __init__(self, val=0):
val = np.array(val) if isinstance(val,(list, np.ndarray)) else np.array([val])
self.val = val.astype('float32')
def __invert__(self): # ~x NOT
return Fuzzy(1-self.val)
def __and__(self, other): # x & y AND
return Fuzzy( np.minimum(self.val, other.val) )
def __or__(self, other): # x | y OR
return Fuzzy( np.maximum(self.val, other.val) )
def __eq__(self, other):
return Fuzzy(self.val == other.val)
def __str__(self):
return f"{self.val[0]}" if len(self.val)==1 else f"{self.val}"
def minmax(self):
return (self.val.min(), self.val.max())
def __gt__(self, other):
return Fuzzy( np.minimum( np.ones_like(self.val), 1-self.val+other.val) )
Пример его использования:
x = Fuzzy( [0, 0, 0, 0.5,0.5,0.5,1, 1, 1] ) y = Fuzzy( [0, 0.5,1, 0, 0.5,1, 0, 0.5,1] ) print(x & y ) # [0. 0. 0. 0. 0.5 0.5 0. 0.5 1. ] print(x | y ) # [0. 0.5 1. 0.5 0.5 1. 1. 1. 1. ]Проверка тождеств булевой алгебры:
vals = np.linspace(0,1,101, dtype='float32') x = Fuzzy(vals) print ( (x & x).minmax() ) # (0.0, 1.0) print ( (x & ~x).minmax() ) # (0.0, 0.5) print ( (x | ~x).minmax() ) # (0.5, 1.0) x, y, z = np.meshgrid(vals, vals, vals) x, y, z = Fuzzy(x), Fuzzy(y), Fuzzy(z) print ( ((x & (y | z)) == ((x & y) | (x & z))).minmax() ) # (1.0, 1.0)