ML: Теория вероятностей
Введение
В задачах машинного обучения и искусственного интеллекта важную роль играют вероятностные соображения. Например, байесовские методы применяются при решении задач классификации и принятии решений. Марковские модели широко используются для обработки естественного языка. Наконец, такое понятие как кросс-энтропия лежит в основе наиболее популярной функции ошибки при работе с нейронными сетями.
Этот документ посвящён неформальному введению в теорию вероятностей и начинает серию материалов, посвящённых вероятностному подходу в машинном обучении и искусственном интеллекте.
Совместная и условная вероятности
Пусть произведено $N$ независимых наблюдений ( = испытаний) в которых событие $A$ наступило $N(A)$ раз и $N-N(A)$ раз не наступило. Эмпирической вероятностью $P(A)$ события $A$ называют частоту его появления: $$ P(A) = \frac{N(A)}{N}. $$ Если в наблюдении могут произойти два события $A$, $B$, то совместной вероятностью наступления, и $A$, и $B$ называют отношение числа наблюдений, когда события происходят одновременно $N(A,\,B)$ к общему числу наблюдений $N$: $$ P(A\,\&\,B) \equiv P(A,\,B) = \frac{N(A,\,B)}{N}. $$
Пусть нас интересует вероятность наступления события $A$,
если в этом же наблюдении происходит событие $B$.
Для этого необходимо подсчитать число $N(A,\, B)$ случаев среди $N(B)$ наблюдений,
когда произошло $B$.
Их отношение называется условной вероятностью:
$$
P(B\to A) ~=~
\frac{N(A,\,B)}{N(B)} ~=~
\frac{P(A\,\&\,B)}{P(B)}.
$$
Обычно условную вероятность обозначают как $P(A\mid B)$, однако для наших целей будет удобнее
введенное выше обозначение (оно особенно естественно в вероятностной логике
и байесовских сетях).
Условная вероятность играет важную роль для характеристики степени "скоррелированности" событий $A$ и $B$. Если всегда, когда происходит $B$, происходит и $A$, то $P(B\to A)=1$. Если же при наступлении $B$, событие $A$ никогда не происходит, то $P(B\to A)=0$. Событие $A$ считается независимым от $B$, когда условная вероятность совпадает с обычной: $P(B\to A)=P(A)$. Стоит проверить, что, если $P(A)\neq P(B)$, то и $P(B\to A) \neq P(A\to B)$.
◊ На стол бросают игральную кость (это наблюдение) и получают одно из шести чисел $\{1,2,3,4,5,6\}$.
Событие $A:$ "выпало 1".
Событие $B:$ "выпало нечётное число": $\{1,3,5\}$ (одно из этих чисел):
 $$
P(A) = \frac{1}{6},~~~~~~~~P(B) = \frac{1}{2},~~~~~~~~P(A\,\&\,B) = \frac{1}{6},
~~~~~~~P(B\to A) = \frac{1}{3},~~~~~~~P(A\to B) = 1.
$$
Вероятности записаны в предположении, что кубик честный (симметричный) и все шесть
чисел выпадают с одинаковой частотой $1/6$.
Это означает, что при большом числе наблюдений $N$ каждая цифра на кубике выпадет
примерно равное число раз $N/6$.
Событие $A\,\&\,B$ возникает только, когда выпадает $\{1\}$
и, например, $P(B\to A)$ по определению равна $P(A\,\&\,B)/P(B)=(N/6)/(N/2) = 1/3$.
$$
P(A) = \frac{1}{6},~~~~~~~~P(B) = \frac{1}{2},~~~~~~~~P(A\,\&\,B) = \frac{1}{6},
~~~~~~~P(B\to A) = \frac{1}{3},~~~~~~~P(A\to B) = 1.
$$
Вероятности записаны в предположении, что кубик честный (симметричный) и все шесть
чисел выпадают с одинаковой частотой $1/6$.
Это означает, что при большом числе наблюдений $N$ каждая цифра на кубике выпадет
примерно равное число раз $N/6$.
Событие $A\,\&\,B$ возникает только, когда выпадает $\{1\}$
и, например, $P(B\to A)$ по определению равна $P(A\,\&\,B)/P(B)=(N/6)/(N/2) = 1/3$.
☝ Требование независимости испытаний означает, что результаты данного испытания не зависят от
результатов предыдущих. Говорят, что испытания должны проводиться в одинаковых (но не тождественных!) условиях.
Например, для получения $P(A)=1/6$, где $A:$ "на кубике выпала единица",
"честный кубик" необходимо также бросать "честно", т.е. проводить случайный эксперимент.
При этом возникает порочный круг в определении случайного характера каждого испытания
и случайный эксперимент является лишь математической моделью физической реальности.
☝ Испытание не обязательно состоит из одного действия. Например, пусть пять раз подбрасывают монету у которой на одной стороне написан $0$, а на второй $1$. Одним испытанием будет последовательность типа $01001$. Всего возможно $2^5 = 32$ результатов испытаний. Если монета "честная" (симметричная) и "честен" способ её подбрасывания, то все последовательности равновероятны. В частности $00000$ будет возникать с такой же частотой ($P=1/32$), как и, например, $10101$. Хотя событие $A$: "число нулей в последовательности равно $3$ или $2$", будет происходить в $20$ раз чаще, чем событие $B$: "выпадает $00000$". При этом $A$ и $B$ несовместные события, т.е. они никогда не происходят одновременно: $P(A\,\&\,B) = 0$. Стоит выписать все $32$ комбинации и посчитать число тех из них, которые благоприятны событию $A$.
Другой пример - монета подбрасывается до тех пор, пока не сравняются число нулей и единиц. В этом случае, результатами испытаний будут последовательности переменной длины типа $01$ или $001011$, но не $0101$.
☝ Важно помнить, что совместность событий $A\,\&\,B$ не означает их одновременности. Например, пусть на стол $N$ раз бросают два игральных кубика разного цвета и событие $A$ означает выпадение шестёрки на зелёном кубике и событие $B$: единицы на синем. Вероятность $P(A\,\&\,B)=1/36$ не зависит от того, кидают кубики одновременно или по-очереди (считая при этом одним наблюдением нахождение на столе обоих кубиков после броска/бросков).
Аналогично условная вероятность $P(B\to A)$ не подразумевает, что событие $B$ происходит раньше события $A$. Выше событием $B$ может быть выпадение 1-цы на втором бросаемом кубике, а событие $A$ - 6-ки на первом кубике.
☝ Слова "эмпирическая вероятность" означают, что отношение $N(A)/N$ является лишь оценкой "истинной" вероятности. Эта оценка тем лучше, чем больше $N$. Пусть "истинная" вероятность (по "бесконечному" числу наблюдений) равна $p_A$. Тогда дисперсия эмпирической вероятности по $N$ наблюдениям равна $p_A\,(1-p_A)/N$ и ошибка в измерении вероятности с ростом $N$ убывает достаточно медленно: $$ P(A) ~=~ \frac{N(A)}{N} ~\pm~ \sqrt{\frac{p_A\,(1-p_A)}{N}}. $$
"Истинная" (математическая) вероятность $p_A$ является абстракцией, предполагающей, что каждое событие обладает такой числовой характеристикой. Однако в макромире - это "сферический конь в вакууме". С натяжкой они существуют для симметричных процессов (монета, рулетка). Хотя на практике стационарность (неизменность во времени) эмпирических вероятностей выполняется достаточно редко. Стоит, например, вспомнить успехи Смока Беллью в "Оленьем Роге" при игре в рулетку.
"Строгая математика" частотному определению вероятности предпочитает аксиоматическое определение, в котором вероятности элементарных событий задаются, а затем уже со всей строгостью вычисляются вероятности составных событий. В реальном же мире необходимо соблюдать баланс между строгостью и практичностью.
Вероятности, логика и теория множеств
Многие соотношения теории вероятностей легко выводятся при помощи геометрических соображений. Представим все проведенные испытания одинаковыми квадратиками внутри квадрата единичной площади, который назовём пространством испытаний. Пометим испытания, в которых происходило событие $A$, как заштрихованную область $A$ (ниже первый рисунок). Испытания не попавшие в эту область соответствуют событию, когда "$A$ не было" или "не $A$". Их будем обозначать в логической нотации как $\neg A$ или чертой сверху: $\bar{A}$. Понятно, что вероятность (площадь) "не $A$" равна $P(\bar{A}) = 1 - P(A)$. Заметим, что обратное неверно: из $P(B)=1-P(A)$ не следует, что $B=\bar{A}$ (постройте опровергающую картинку).
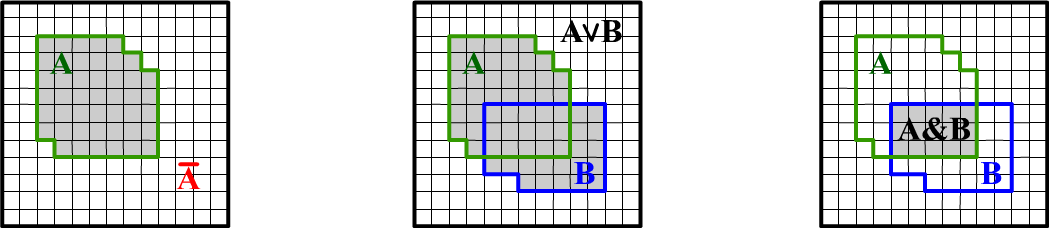
Если в испытании происходит или $A$, или $B$, или оба события, то вероятность $P(A\vee B)$ или $P(A\cup B)$ равна закрашенной области объединяющей оба события (второй рисунок). Логическая нотация $A\vee B$ и теоретико-множественная $A \cup B$ эквивалентны. В первом случае мы подчёркиваем, что утверждение о наступлении событий формируется при помощи логического союза ИЛИ. Во втором - что множества испытаний, в которых произошли эти события объединяются. Чаще мы будем использовать логические обозначения.
Наступление двух событий $A$ и $B$ в одном испытании соответствует закрашенной области на третьем рисунке. Это пересечение событий $A \cap B$. Площадь такой области равна совместной вероятности $P(A\,\&\,B)$, или просто $P(A,\,B)$. Третий рисунок иллюстрирует также определение условной вероятности $P(B\to A)=P(A\,\&\,B)/P(B)$. Если известно, что произошло событие $B$, то всё пространство испытаний "сжимается" до области $B$ и для события $A$ необходимо подсчитывать только те испытания, которые попали в $B$.
Соотношения между вероятностями
✒ Найдём вероятность объединения двух событий (логическое ИЛИ). Площадь $P(A\vee B)$ равна сумме площадей $P(A)$, $P(B)$, минус площадь их пересечения $P(A\,\&\,B)$, которая при сложении областей посчитана два раза: $$ P(A\vee B) = P(A) + P(B) - P(A\,\&\,B). $$
Подставив вместо $B$ отрицание $\bar{A}$, получаем $P(\bar{A}) = 1 - P(A)$. При этом $A\vee\bar{A}=\mathbb{T}$ - это всё пространство испытаний (квадрат единичной площади), а $A\,\&\,\bar{A}=\mathbb{F}$ - невозможное событие, имеющее нулевую вероятность.
✒
 В логике, дизъюнкция (ИЛИ) и конъюнкция (И) связаны правилом де-Моргана:
$$
~~~~~~~~~~~~~~~~~~~~~~~\neg(A\vee B)=\neg A\,\&\,\neg B
~~~~~~~~\text{ или }~~~~~~~~~~~~
A\vee B=\neg( \bar{A}\,\&\,\bar{B}).
$$
Из него следует ещё одно важное соотношение для вероятности объединения событий:
$$
~~~~~~~~~~~~~~~~~~~~~~~~~P(A\vee B) = 1 - P\bigr(\bar{A}\,\&\,\bar{B}\bigr).
$$
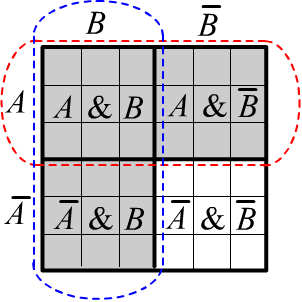
Его иллюстрация приведена на рисунке справа.
Горизонтальная, обведенная красным пунктиром область пространства испытаний - это событие $A$.
Вертикальная, обведенная синей линией область - это событие $B$.
Серым цветом заштриховано их объединение $A\vee B$. Оставшаяся не заштрихованная часть - это отрицание
$A\vee B$ и она же равна $\bar{A}\,\&\,\bar{B}$.
Эту формулу удобно использовать для вычисления объединения большого числа событий:
$$
P(A_1\vee ...\vee A_n) ~=~ 1 - P(\bar{A}_1\,\&\, ...\,\&\, \bar{A}_n).
$$
В логике, дизъюнкция (ИЛИ) и конъюнкция (И) связаны правилом де-Моргана:
$$
~~~~~~~~~~~~~~~~~~~~~~~\neg(A\vee B)=\neg A\,\&\,\neg B
~~~~~~~~\text{ или }~~~~~~~~~~~~
A\vee B=\neg( \bar{A}\,\&\,\bar{B}).
$$
Из него следует ещё одно важное соотношение для вероятности объединения событий:
$$
~~~~~~~~~~~~~~~~~~~~~~~~~P(A\vee B) = 1 - P\bigr(\bar{A}\,\&\,\bar{B}\bigr).
$$
Его иллюстрация приведена на рисунке справа.
Горизонтальная, обведенная красным пунктиром область пространства испытаний - это событие $A$.
Вертикальная, обведенная синей линией область - это событие $B$.
Серым цветом заштриховано их объединение $A\vee B$. Оставшаяся не заштрихованная часть - это отрицание
$A\vee B$ и она же равна $\bar{A}\,\&\,\bar{B}$.
Эту формулу удобно использовать для вычисления объединения большого числа событий:
$$
P(A_1\vee ...\vee A_n) ~=~ 1 - P(\bar{A}_1\,\&\, ...\,\&\, \bar{A}_n).
$$
✒ При помощи рисунка выше несложно проверить, что $P(A\vee B)=P(A)+P(\bar{A}\,\&\,B)$.
Обобщение этого соотношения называется ортогональным разложением дизъюнкции:
$$
P(A_1\vee ...\vee A_n) ~=~ P(A_1) + P(\bar{A}_1,A_2)+...+P(\bar{A}_1,...,\bar{A}_{n-1},A_n).
$$
Оно доказывается по индукции при помощи предыдущего соотношения ($n=2$).
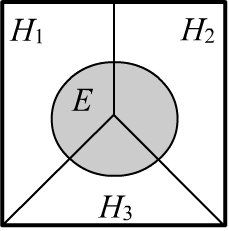 ✒ Рассмотрим множество $\{H_1,...,H_n\}$ непересекающихся событий: $H_i\,\&\,H_j=\mathbb{F}\equiv\varnothing$,
которые называются несовместными. Для таких событий
справедливо соотношение:
$$
P(H_1\vee H_2\vee...\vee H_n) = P(H_1)+P(H_2)+...+P(H_n).
$$
Пусть несовместные события покрывают всё пространство испытаний, проводя его разбиение (справа случай для $n=3$).
В этом случае выполняется нормировочное условие:
$$
\sum_iP(H_i) = 1.
$$
Кроме этого, для любого события $E$ справедлива
формула полной вероятности:
$$
P(E) = \sum_i P(H_i \,\&\, E) = \sum_i P(H_i)\,P(H_i\to E),
~~~~~~~~~~~~~~~~~~
$$
где учтено определение условной вероятности. В частном случае для любых двух событий:
$$
P(A) ~=~ P(A,\,B)+P(A,\,\bar{B}) ~=~ P(B)\,P(B\to A)\,+\,P(\bar{B})\,P(\bar{B}\to A),
$$
где $B$ и $\bar{B}$ разбивают всё пространство испытаний на две непересекающиеся области.
✒ Рассмотрим множество $\{H_1,...,H_n\}$ непересекающихся событий: $H_i\,\&\,H_j=\mathbb{F}\equiv\varnothing$,
которые называются несовместными. Для таких событий
справедливо соотношение:
$$
P(H_1\vee H_2\vee...\vee H_n) = P(H_1)+P(H_2)+...+P(H_n).
$$
Пусть несовместные события покрывают всё пространство испытаний, проводя его разбиение (справа случай для $n=3$).
В этом случае выполняется нормировочное условие:
$$
\sum_iP(H_i) = 1.
$$
Кроме этого, для любого события $E$ справедлива
формула полной вероятности:
$$
P(E) = \sum_i P(H_i \,\&\, E) = \sum_i P(H_i)\,P(H_i\to E),
~~~~~~~~~~~~~~~~~~
$$
где учтено определение условной вероятности. В частном случае для любых двух событий:
$$
P(A) ~=~ P(A,\,B)+P(A,\,\bar{B}) ~=~ P(B)\,P(B\to A)\,+\,P(\bar{B})\,P(\bar{B}\to A),
$$
где $B$ и $\bar{B}$ разбивают всё пространство испытаний на две непересекающиеся области.
✒ Следующее важное соотношение называется цепным правилом:
$$
P(A_1,A_2,...,A_n) = P(A_1)\cdot P(A_1\to A_2)\cdot P(A_1,A_2\to A_3)\cdot...\cdot P(A_1,...,A_{n-1}\to A_n).
$$
Его несложно доказать, подставляя определения $P(A_1,A_2\to A_3)=P(A_1,A_2, A_3)/P(A_1,A_2)$, и т.д.
Цепное правило можно интерпретировать так:
чтобы в испытании одновременно наступили события $A_1,...,A_n$, необходимо, чтобы случилось $A_1$;
если это произошло, то должно произойти $A_2$, т.е. $A_1\to A_2$ и т.д.
Понятно, что порядок в котором выбираются события для цепного правила может быть произвольным.
✒ (*) В заключение приведём формулу для дизъюнкции $n$ событий: $$ P(A_1\vee A_2\vee...\vee A_n) = \sum^n_{i=1} P(A_i) - \sum_{1 \le i\lt j\le n} P(A_i,A_j) + \sum_{1 \le i\lt j \lt k\le n} P(A_i,A_j,A_k) - ... +(-1)^{n+1} P(A_1,A_2,...,A_n). $$ Она доказывается по индукции, при помощи соотношения $P(A\vee B)=P(A)+P(B)-P(A,B)$ (случай $n=2$), в которой следует положить $A=A_1\vee...\vee A_n$ и $B=A_{n+1}$. Затем необходимо учесть дистрибутивность дизъюнкции и конъюнкции $(A_1\vee...\vee A_n)\,\&\,A_{n+1}=(A_1\,\&\,A_{n+1})\,\vee...\vee\, (A_n\,\&\,A_{n+1})$ и закон поглощения $A_{n+1}\,\&\,A_{n+1}=A_{n+1}$.
Немного неравенств *
✒ Используя формулу полной вероятности $P(A) = P(A\,\&\,B) + P(A\,\&\,\bar{B})$ и положительность вероятностей заключаем, что $P(A) ~\ge~ P(A\,\&\,B)$ и аналогичное неравенство для $B$. Кроме этого, из $A\,\&\,B=\neg\neg(A\,\&\,B)$ или $$P(A\,\&\,B)=1-P(\neg(A\,\&\,B))=1-P(\bar{A}\vee \bar{B})= 1-P(\bar{A})-P(\bar{B})+P(\bar{A}\,\&\,\bar{B})= P(A)+P(B)-1+P(\bar{A}\,\&\,\bar{B}), $$ следует, что $P(A\,\&\,B)$ больше, чем $P(A)+P(B)-1$. В результате получаем следующее ограничение на вероятность совместного наступления двух событий (см. также иллюстрацию справа):
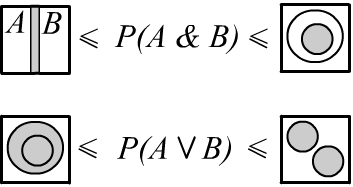 $$
\max[0,~P(A)+P(B)-1]~~~\le~~~ P(A\,\&\,B) ~~~\le~~~ \min[P(A),\,P(B)].~~~~~~~~~~~
$$
$$
\max[0,~P(A)+P(B)-1]~~~\le~~~ P(A\,\&\,B) ~~~\le~~~ \min[P(A),\,P(B)].~~~~~~~~~~~
$$
Аналогично для диапазона вероятности объединения двух событий: $$ \max[P(A),\,P(B)]~~~~~~~~\le~~~~~~ P(A\vee B) ~~~\le~~~\min[1,~P(A)+P(B)]. $$
Пространство испытаний достаточно "тесное", поэтому если $P(A)$ или $P(B)$ заметно отличны от $1/2$ (лучше оба и в одну сторону), то данные не неравенства дают узкие интервалы для конъюнкции ($\&$) и дизъюнкции ($\vee$). В различных вариантах нечёткой логики используются верхние или нижние границы этих интервалов для оценки конъюнкции и дизъюнкции двух нечётких высказываний. Естественно, неравенства не учитывают возможную связь между событиями. Так, если $B=\bar{A}$, то $P(A\,\&\,B)=0$ оказывается на нижней границе интервала, а $P(A\vee B)=1$ - на верхней.
| $P(A)$ | $P(B)$ | $P(A\,\&\,B)$ | $P(A\vee B)$ |
| $0.5$ | $0.9$ | $[0.4,\,0.5]$ | $[0.9,\,1.0]$ |
| $0.5$ | $0.1$ | $[0.0,\,0.1]$ | $[0.5,\,0.6]$ |
| $0.3$ | $0.7$ | $[0.0,\,0.3]$ | $[0.7,\,1.0]$ |
| $0.5$ | $0.5$ | $[0.0,\,0.5]$ | $[0.5,\,1.0]$ |
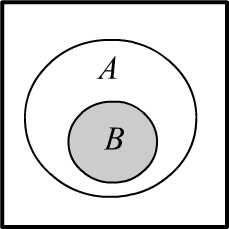 ✒ Пусть выполняется соотношение $P(A\,\&\,B)\,=\,P(B)$.
Тогда область события $B$
является подмножеством ($B\subset A$) области события $A$. В этом случае:
$$
P(B) \le P(A) \le 1.
$$
Из определения $P(B\to A)=P(A\,\&\,B)/P(B)$ следует $P(B\to A)=1$.
Это означает, что всегда, когда происходит событие $B$, обязательно произойдёт и событие $A$
($B$ влечёт за собой $A$).
✒ Пусть выполняется соотношение $P(A\,\&\,B)\,=\,P(B)$.
Тогда область события $B$
является подмножеством ($B\subset A$) области события $A$. В этом случае:
$$
P(B) \le P(A) \le 1.
$$
Из определения $P(B\to A)=P(A\,\&\,B)/P(B)$ следует $P(B\to A)=1$.
Это означает, что всегда, когда происходит событие $B$, обязательно произойдёт и событие $A$
($B$ влечёт за собой $A$).
✒ Докажем ещё одно неравенство, которое находит применение в вероятностной логике: $$ P(A\to B)~~\le~~P(\bar{A}\vee B). $$ Записав формулу для дизъюнкции и полной вероятности $P(B)=P(A,B)+P(\bar{A},B)$ имеем: $$ P(\bar{A}\vee B)=P(\bar{A})+P(B)-P(\bar{A},B)=1-P(A)+P(A,B)+P(\bar{A},B)-P(\bar{A},B) = 1-P(A)\,\bigr(1-P(A\to B)\bigr). $$ Отсюда следует $1-P(\bar{A}\vee B) = P(A)\,\bigr(1-P(A\to B)\bigr)$ и так как $P(A)\le 1$, получаем требуемое неравенство.
Множество элементарных событий
 Элементарным
называют событие которое нельзя представить как объединение других событий.
Элементарным
называют событие которое нельзя представить как объединение других событий.
В данном испытании всегда происходит одно и только одно элементарное
событие (все они попарно несовместны и одно из них обязательно произойдёт).
Множество элементарных событий $\{E_1,...,E_n\}$
обозначают буквой $\Omega$. При этом $P(\Omega)=1$ и $P(E_i\, \&\, E_j)=0,~i\neq j$.
Любое событие $A$ является подмножеством множества элементарных событий: $A\subset \Omega$.
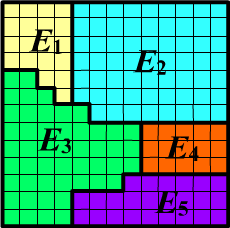
◊ Произвольные события могут пересекаться. Например, для $\Omega=\{E_1,E_2,E_3,E_4,E_5\}$ и составных событий $A=\{E_1,E_3,E_5\}$, $B=\{E_1,E_2,E_3\}$ имеем $A\,\&\,B=\{E_1,E_3\}$. Фигурные скобки для $A\,\&\,B$ в данном случае обозначают исключающее логическое ИЛИ (произошло или $E_1$, или $E_3$).
Задача в теории вероятности полностью определена, если известно множество элементарных событий и заданы их вероятности. Считается, что процедура задания этих вероятностей лежит вне теории.
◊ Пусть в примере выше заданы вероятности элементарных событий $\{P_1,\,P_2,\,P_3,\,P_4,\,P_5\}$, сумма которых равна единице. Тогда $P(A)=P_1+P_3+P_5$, а $P(A\,\&\,B)=P_1+P_3$.
☝ Подчеркнём отличие элементарных событий от произвольного разбиения пространства испытаний. Элементарные события так разбивают пространство, чтобы любое событие могло быть выражено через их объединение. Множество $\Omega$ с $|\Omega| = n$ элементами имеет $2^{n}$ подмножеств (включая пустое $\varnothing$ и само $\Omega$). Множество этих подмножеств обозначается как: $2^{\Omega}$. Для нумерации подмножеств можно использовать бинарные числа типа $10101$, что, для примера выше, означает $A=\{E_1,E_3,E_5\}$.
Набор произвольных событий, в свою очередь, порождает множество элементарных событий. Пусть, например, в испытаниях могут происходить только события $A$ и $B$. Тогда множество элементарных событий будет состоять из четырёх элементов $\{ A\,\&\,B,~A\,\&\,\bar{B},~\bar{A}\,\&\,B,~\bar{A}\,\&\,\bar{B}\}$, где отсутствие событий $\bar{A}\,\&\,\bar{B}$ в испытании также считается событием. Если какие-то из этих сочетаний невозможны, то множество элементарных событий уменьшается. В общем случае $n$ событий могут порождать не более чем $2^n$ несовместных элементарных событий.
 ◊ На стол бросают (одновременно или последовательно) две монеты различного размера.
Тогда множество элементарных событий равно $\Omega = \{00,\, 01,\, 10,\, 11\}$, где
$0$ - "герб", а $1$ - "число" и первым идёт значение, например, на меньшей монете.
Из соображений симметрии, для честных монет и способа их бросания,
вероятности всех четырёх элементарных событий равны $1/4$.
◊ На стол бросают (одновременно или последовательно) две монеты различного размера.
Тогда множество элементарных событий равно $\Omega = \{00,\, 01,\, 10,\, 11\}$, где
$0$ - "герб", а $1$ - "число" и первым идёт значение, например, на меньшей монете.
Из соображений симметрии, для честных монет и способа их бросания,
вероятности всех четырёх элементарных событий равны $1/4$.
Если же монеты одинаковы и неразличимы, то множество элементарных событий состоит из трёх элементов: $\Omega = \{00,\, 01,\, 11\}$ (два герба, один герб и одно число, два числа). При этом $P(00)=P(11)=1/4$ и $P(01)=1/2$, где последняя вероятность является вероятностью объединения элементарных событий $01,\, 10$ для различимых монет в одно элементарное событие для неразличимых монет.
Заметим, что это "очевидное" рассуждение не было очевидным на заре построения теории вероятности. Тогда считалось, что для одинаковых монет элементарные события $\{00,\, 01,\, 11\}$ должны быть равновероятными ($1/3$). На самом деле то, что неразличимые монеты "в принципе можно различить" и вероятность $P(01 \vee 10)=1/2$, а не $1/3$ - это не математический, а физический (экспериментальный) факт. Он справедлив в макромире, однако в микромире это уже не так, что сказывается в различии статистических распределений Бозе и Максвелла.
 ◊ В закрытой урне находятся четыре белых ($w$) и один чёрный ($b$) шар.
Сначала случайно выбирают один шар, а затем второй (шары в урну не возвращают).
Одно испытание - это последовательность
и возможны 4 элементарных события:
$\Omega = \{ w_1w_2,\,w_1b_2,\,b_1w_2,\,b_1b_2 \}$ (сначала белый, затем снова белый и т.д.).
Их вероятности равны:
$$
P(w_1w_2) = \frac{4}{5}\,\frac{3}{4}=\frac{3}{5},~~~~
P(w_1b_2) = \frac{4}{5}\,\frac{1}{4}=\frac{1}{5},~~~~
P(b_1w_2) = \frac{1}{5}\,1=\frac{1}{5},~~~~
P(b_1b_2) = \frac{1}{5}\,0=0.
$$
Действительно, вероятность достать первым белый шар равна $P(w_1)=4/5$.
После этого в урне остаётся 3 белых шара и 1 чёрный. Вероятность снова достать белый равна $P(w_1\to w_2)=3/4$.
По определению условной вероятности $P(w_1,w_2)=P(w_1)\,P(w_1\to w_2)$, что даёт $(4/5)\cdot(3/4)$. Аналогично для остальных вариантов.
◊ В закрытой урне находятся четыре белых ($w$) и один чёрный ($b$) шар.
Сначала случайно выбирают один шар, а затем второй (шары в урну не возвращают).
Одно испытание - это последовательность
и возможны 4 элементарных события:
$\Omega = \{ w_1w_2,\,w_1b_2,\,b_1w_2,\,b_1b_2 \}$ (сначала белый, затем снова белый и т.д.).
Их вероятности равны:
$$
P(w_1w_2) = \frac{4}{5}\,\frac{3}{4}=\frac{3}{5},~~~~
P(w_1b_2) = \frac{4}{5}\,\frac{1}{4}=\frac{1}{5},~~~~
P(b_1w_2) = \frac{1}{5}\,1=\frac{1}{5},~~~~
P(b_1b_2) = \frac{1}{5}\,0=0.
$$
Действительно, вероятность достать первым белый шар равна $P(w_1)=4/5$.
После этого в урне остаётся 3 белых шара и 1 чёрный. Вероятность снова достать белый равна $P(w_1\to w_2)=3/4$.
По определению условной вероятности $P(w_1,w_2)=P(w_1)\,P(w_1\to w_2)$, что даёт $(4/5)\cdot(3/4)$. Аналогично для остальных вариантов.
Положив в урну $M$ белых шаров и $N-M$ чёрных, стоит проверить, что всегда $P(w_1,b_2)=P(b_1,w_2)$. Так и должно быть, потому, что "посмотреть" на цвет вытащенных шаров можно уже в конце (перемешав их).
Если нас интересует только второй шар, то можно просуммировать вероятности элементарных событий по первому шару: $P(w_2)=P(w_1,\,w_2)+P(b_1,\,w_2)=4/5$ = вероятность достать вторым белый шар. Условная вероятность достать первым чёрный шар, если вторым был белый, равна $P(w_2\to b_1) = P(b_1,\,w_2)/P(w_2)=1/4$.
◊ Есть две урны. В первой урне $5$ шаров из которых $4$ белых и $1$ чёрный. Во второй урне $2$ белых и $2$ чёрных шара. Из первой урны случайно выбирают два шара и перекладывают их во вторую урну. Какова вероятность затем вытащить из второй урны белый шар?
Пусть $w_1b_2w$ означает, что из первой урны сначала достали белый шар ($w_1$), затем чёрный ($b_2$), переложили их во вторую урну, откуда после этого достали белый шар ($w$). Множество элементарных событий состоит из восьми элементов: $\Omega=\{w_1w_2w,\,w_1b_2w,\,b_1w_2 w,\,b_1b_2 w,\,w_1w_2b,\,w_1b_2b,\,b_1w_2 b,\,b_1b_2 b\}$. Вероятности этих событий вычисляются при помощи цепного правила: $P(x_1x_2x)=P(x_1)P(x_1\to x_2)P(x_1,x_2\to x)$. В результате получается: $P=\{4,\,1,\,1,\,0,\,2,\,1,\,1,\,0\}/10$. Сумма (объединение) первых четырёх событий благоприятствует доставанию в конце белого шара и её вероятность равна $6/10=3/5$.
◊ Известно, что некто выиграл в лотерею один из трёх возможных призов: $W_1,W_2,W_3$.
Вероятности таких выигрышей равны $P(W_i)$ и $P_0$ - вероятность проигрыша.
Какова вероятность того, что был выигран третий приз?
Множество элементарных событий состоит из $\{W_0,W_1,W_2,W_3\}$. Нам необходимо вычислить
условную вероятность:
$$
P(W_1\vee W_2\vee W_3 \to W_3)= \frac{P\bigr((W_1\vee W_2\vee W_3) \,\&\, W_3\bigr)}{P(W_1\vee W_2\vee W_3)}=\frac{P(W_3)}{P(W_1)+P(W_2)+P(W_3)}.
$$
Так как элементарные события несовместны, выше учтено, что $W_1\,\&\,W_3=W_2\,\&\,W_3=\varnothing$ и $W_3\,\&\,W_3=W_3$.
Таблицы вероятностей
Название события обозначим заглавной буквой $A$, а прописными буквами $a,\bar{a}$ - его два возможных "значения": $A=a$ - событие произошло и $A=\bar{a}$ - не произошло. Тогда вероятности $P(a)$ и $P(\bar{a})=1-P(a)$ будут числами, а $P(A)$ - вектором с компонентами $\{P(a),P(\bar{a})\}$ или функцией в которую надо подставить $a$ или $\bar{a}$.
Пусть, в общем случае, нас интересует $n$ событий $\{X_1,...,X_n\}$. Тогда $2^n$ вероятностей $P(X_1,...,X_n)$, где $X_i = x_i$ (событие происходит) или $X_i = \bar{x}_i$ (событие не происходит) полностью определяют задачу. Каждая такая вероятность характеризует элементарное событие. Зная эти числа, можно ответить на любой вопрос. Например, вероятность $P(X_1,X_2)$ равна сумме $P(X_1,...,X_n)$ по возможным "значениям" событий $X_3,...,X_n$ и т.д.
| $s$ | $\bar{s}$ | Tot | |
|---|---|---|---|
| $b$ | 8 | 2 | 10 |
| $\bar{b}$ | 32 | 58 | 90 |
| Tot | 40 | 60 | 100 |
Во введенных выше обозначениях $P(b\to S)$ является функцией от $S$ с 2-я значениями для $S=s$ и $S=\bar{s}$: $$ P(b\to S) ~=~ \bigr\{ p(b \to s),~~~p(b\to \bar{s})\bigr\} ~=~ \bigr\{ 8,~~~2\bigr\}/10. $$ При этом $P(B\to S)$ является уже матрицей $2\times 2$ c компонентами $P(b\to s)$, $P(b\to \bar{s})$, $P(\bar{b}\to s)$, $P(\bar{b}\to \bar{s})$.
Найдём вероятность того, что встреченный человек окажется не блондинкой или умным. С точки зрения логики $\bar{B} \vee S = \neg\neg(\bar{B}\vee S) = \neg(B\,\&\,\bar{S})$. Поэтому: $$ P(\bar{b} \vee s ) = 1- P(b,\,\bar{s}) = 1-\frac{2}{100} = 0.98. $$ Этот результат можно также получить при помощи тождества: $$ P(\bar{b} \vee s) = P(\bar{b}) + P(s) - P(\bar{b},\, s) = \frac{90}{100} + \frac{40}{100} - \frac{32}{100} = \frac{98}{100} $$ или просто просуммировав соответствующие объединению событий числа: $(32+58+8)/100$ из второй строки и первого столбца (без повторов).
Случайные величины
Пусть величина $X$ в каждом испытании принимает одно из значений, принадлежащих некоторому множеству. Если множество счётно, например, $\{x_1,...,x_n\}$, то $X$ называется дискретной случайной величиной. Если значения $X$ - вещественные числа, то это непрерывная случайная величина.
◊ Выпадение числа на кубике можно рассматривать как дискретную случайную величину с шестью возможными значениями $X=x \in\{1,2,3,4,5,6\}$. Точка на столе, куда падает кубик, является непрерывной векторной случайной величиной с двумя компонентами $\mathbf{X}=\mathbf{x}=\{x_1,x_2\}$ (координаты кубика).
Случайную величину принято обозначать заглавным шрифтом $X$, а её значения - прописным $x$. Вероятности, с которыми в испытании появляются значения, называют распределением вероятностей (дискретным или непрерывным): $P(X=x)$. Кратко это записывается в виде функции $p(x)$.
Событие является частным случаем дискретных случайных величин с двумя значениями ($1$ - событие произошло или $0$ - событие не произошло). Вместо записи $P(A=1)$ выше мы писали $P(a)$, а для $P(A=0)$ - $P(\bar{a})$. Множество элементарных событий $E=e \in \Omega=\{E_1,...,E_n\}$ является случайной величиной (в данном испытании происходит ровно одно событие, т.е. $E$ имеет определённое значение из множества $\Omega$). С другой стороны, дискретную случайную величину можно рассматривать как событие с двумя несовместными исходами: $P(X=x)$ или $P(X\neq x)$.
Так как случайная величина принимает конкретное значение в каждом испытании, сумма вероятностей распределения должна равняться единице. Это условие нормировки записывается различным образом для дискретных и непрерывных величин: $$ \sum_i p(x_i)=1,~~~~~~~~~~~~~~~~~~~~~~\int\limits_X p(x)\,dx = 1. $$ Во втором случае функцию $p(x)$ называют плотностью вероятности, а $p(x)\,dx$ - это вероятность того, что случайная величина окажется в диапазоне $[x,\,x+dx]$. Интегрирование ведётся по всей области возможных значений $X$. Далее для краткости будем говорить о дискретных величинах. В случае непрерывных случайных величин, во всех формулах необходимо заменить $p(x_i)$ на $p(x)\,dx$, а сумму на интеграл.
✒ Средним значением (mean) $X_\text{ср}$ случайное величины называется взвешенная на вероятности сумма её возможных значений. Усреднение квадратов отклонении от среднего (variance) называется дисперсией $D$: $$ X_\text{ср}\equiv \langle X \rangle = \sum_i x_i\, p(x_i),~~~~~~~~~~~~D = \langle (X-X_\text{ср} )^2 \rangle = \sum_i (x_i-X_\text{ср})^2\, p(x_i). $$ Чем вероятнее значение случайной величины, тем больший вклад в среднее оно даёт. Если распределение вероятностей $p(x)$ имеет единственный симметричный максимум, то среднее характеризует его положение, а корень из дисперсии $\sigma=\sqrt{D}$ (среднеквадратичное отклонение) - ширину максимума.
Непосредственно из определения следует, что дисперсию можно вычислить также по такой формуле: $$ D = \langle (X-X_\text{ср} )^2 \rangle = \langle X^2-2X\,X_\text{ср}+X^2_\text{ср} \rangle =\langle X^2\rangle-2\langle X\rangle\,X_\text{ср}+X^2_\text{ср} = \langle X^2\rangle - X^2_\text{ср}, $$ где учтено, что среднее суммы равно сумме средних, а постоянный множитель (константу) $X_\еуче{ср}$ можно выносить за знак среднего (за сумму). Обратим внимание, что, если $D \neq 0$, то среднее квадрата случайной величины не равно квадрату её среднего: $$ \langle X+Y\rangle = \langle X\rangle + \langle Y\rangle,~~~~~~~~~ \langle \alpha\,X\rangle = \alpha\,\langle X\rangle,~~~~~~~~~ \langle X^2\rangle \neq \langle X\rangle^2. $$
◊ Кубик бросают до тех пор, пока не выпадет $6$. Вычислить среднее число бросков в таком эксперименте.
Случайной величиной $N$ является число бросков.
Вероятность получить $n-1$ не шестёрок, а затем шестёрку будет $(5/6)^{n-1}(1/6)$.
Поэтому средняя длина равна
(при суммировании используем бесконечный ряд $x^n$, равный $1/(1-x)$ и его производную $n\, x^{n-1}$,
сумма которой равна $1/(1-x)^2$):
$$
N_{ср} = \sum^\infty_{n=1} n\, \left(\frac{5}{6}\right)^{n-1}\,\frac{1}{6} = 6.
$$
Существует
изящное рассуждение не требующее суммирования.
Результаты $K$ экспериментов "состыкуем" в одну последовательность
типа $4125\mathbf{6}115323\mathbf{6}...$
Шестёрки в ней будут встречаться с вероятностью $1/6$, поэтому длина $L$ последовательности
равна $6\cdot K$, а средняя длина одного эксперимента: $L/K=6$.
Независимость событий
События $A,B$ называют независимыми, если условная вероятность $A$ не зависит от факта наступления события $B$, а вероятность $B$ от наступления $A$: $$ P(B \to A)=P(A),~~~~~~~~~~~~~P(A \to B)=P(B). $$ Если в $N$ испытаниях нас не интересует $B$, то $P(A)=N(A)/N$. Если же мы отбираем только те испытания, в которых произошло $B$, то $P(B\to A)=N(A,\,B)/N(B)$. Когда эти две величины совпадают, это и означает, что вероятность $A$ не зависит от того интересовались мы $B$ или нет (= $A$ не зависит от $B$).
Из определения условной вероятности следует, что совместная вероятность независимых событий
равна:
$$
P(A,\,B)=P(A)\cdot P(B).
$$
Независимость событий обозначают следующим образом: $A\Prep B$
(совместная вероятность "разделяется").
Если $P(A,\,B,\,C)=P(A)\cdot P(B)\cdot P(C)$, то это $A\Prep B \Prep C$ (три независимых события).
Очевидно, что несовместные события $P(A,B)=0$ всегда независимы, если, конечно, $P(A),P(B) \gt 0$.
☝ Иногда независимость интуитивно очевидна, когда между событиями нет связи (например, при подбрасывании двух монет). Однако она также может быть "случайным" эффектом статистики. Например, пусть во вселенной есть 100 женщин. Из них 10 блондинок $(B)$ и 20 зеленоглазых ($G$). Если зеленоглазых блондинок 2, то события $B$ и $G$ будут независимы. При другом числе $B\,\&\,G$ это уже не так.
Вообще, "зависимость" (не выполнение условия независимости) $P(A,\,B)\neq P(A)\cdot P(B)$ не стоит понимать в обыденном смысле. В частности, факт "зависимости" не означает, что $A$ является причиной $B$ или наоборот. Лучше о независимости думать в терминах условной вероятности $P(A\to B)=P(B)$: "добавляет ли что-либо знание значения $A$ для прогнозирования значения $B$?".
◊ Рассмотрим три события, возникающие при бросании кости, на которой "выпало число ...":
$$
\text{"чётное": } A=\{2,4,6\};~~~~~~~ \text{"делящееся на три":} B=\{3,6\};~~~~~~~\text{"меньшее пяти": }C=\{1,2,3,4\}.
$$
Так как $A\,\&\,B = \{6\}$, $A\,\&\,C = \{2,4\}$, $B\,\&\,C = \{3\}$, несложно проверить, что $A\Prep B$, $A\Prep C$,
но при этом $B$ и $C$ не являются независимыми.
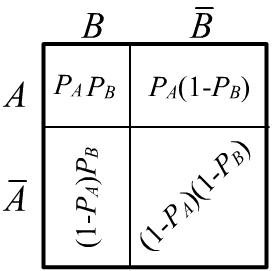 ✒ Пусть два события независимы $A\Prep B$.
Будут ли независимыми их отрицания $\bar{A}\Prep \bar{B}\,$?
✒ Пусть два события независимы $A\Prep B$.
Будут ли независимыми их отрицания $\bar{A}\Prep \bar{B}\,$?
Да, будут. Воспользуемся геометрическими соображениями. Справа приведено множество элементарных событий
в пространстве испытаний.
Событие $A\,\&\,B$ (левый верхний угол) имеет вероятность ("площадь")
$P(A)\,P(B)$. Вся верхняя строка с площадью $P(A)$ соответствует событию $A$.
Поэтому событие $A\,\&\,\bar{B}$ имеет площадь $P(A)-P(A)\,P(B)$. Аналогично для оставшихся двух
элементарных событий $\bar{A}\,\&\,B$ и $\bar{A}\,\&\,\bar{B}.$
✒ Совместные вероятности независимых событий факторизуются $P(A,\,B)=P(A)\,P(B)$. Однако, по-парное выполнение этого соотношения между множеством событий не всегда означает их независимость.
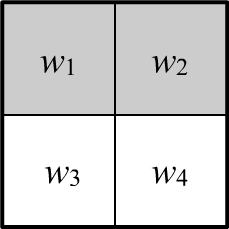 ◊ Пусть есть четыре элементарных равновероятных событий:
$\Omega =\{w_1,\,w_2,\,w_3,\,w_4\}.$
Рассмотрим три составных события $A=\{w_1,w_2\},$ $B=\{w_1,w_3\},$ $C=\{w_1,w_4\}$.
◊ Пусть есть четыре элементарных равновероятных событий:
$\Omega =\{w_1,\,w_2,\,w_3,\,w_4\}.$
Рассмотрим три составных события $A=\{w_1,w_2\},$ $B=\{w_1,w_3\},$ $C=\{w_1,w_4\}$.
Их вероятности равны $1/2$ (на рисунке заштриховано событие $A$).
Так как $A\,\&\,B~=~w_1$, то $P(A\,\&\,B) ~=~ P(w_1) ~=~1/4$, поэтому:
$$
P(A,\,B)=P(A)\,P(B),~~~~~~~~
P(A,\,C)=P(A)\,P(C),~~~~~~~~
P(B,\,C)=P(B)\,P(C).
$$
В тоже время:
$$
P(A,\,B,\,C) = P(w_1) = \frac{1}{4} \neq P(A)\,P(B)\,P(C).
$$
Таким образом, из $A\Prep B$, $A\Prep C$, $B\Prep C$, вообще говоря, не следует $A\Prep B \Prep C$.
✒ Отметим также, что независимость не обладает транзитивностью: $$ A\Prep B,~~B\Prep C~~~~~~\not\Rightarrow~~~~A\Prep C. $$ Например это так для такой совместной вероятности: $P(A,B,C)=P(B)\,P(A,C)$.
✒ Требование $P(X,Y,Z)=P(X)\,P(Y)\,P(Z)$ независимости трёх событий $A\Prep B \Prep C$ включает в себя все парные независимости, если провести суммирование по "ненужному" событию: $$ P(X,Y)~=~\sum_{Z}P(X,Y,Z) ~=~P(X,Y,z)+P(X,Y,\bar{z})~=~P(X)P(Y)\,\bigr(P(z)+P(\bar{z})\bigr)~=~P(X)P(Y), $$ т.к. $P(z)+P(\bar{z})=1$, где $z$ - событие $Z$ произошло, а $\bar{z}$ - не произошло. Поэтому $A\Prep B \Prep C~~~\Rightarrow~~~A\Prep B$ и т.д.
✒ Докажем, что дисперсия частоты события по $N$ испытаниям равна $p_A(1-p_A)/N$. Пусть много раз проводятся эксперименты, в каждом из которых совершается $N$ испытаний по наблюдению события $A$. Величина $X_i=1$, если в $i$-том испытании событие произошло, иначе $X_i=0$. Это случайная величина, т.к. в одном эксперименте, в $i$-м испытании событие может произойти, а в другом - нет. Частота события также становится случайной величиной $P=(X_1+...+X_N)/N$ . Найдём её среднее и дисперсию по всем экспериментам. Если "истинная" вероятность события равна $p_A$, то для любого $i$: $$ \langle X_i \rangle = 1\cdot p_A+0\cdot (1-p_A)=p_A,~~~~~~~~~~~~~~\langle X^2_i \rangle = 1^2\cdot p_A+0^2\cdot (1-p_A)=p_A. $$ Соответственно, средняя частота также равна $P_\text{ср}=\langle P \rangle = p_A$. Случайные величины $X_i$ и $X_j$ являются независимыми (событие может произойти в испытании независимо от того, что происходило в других испытаниях). Поэтому: $$ при~~i\neq j~~~~~~~~~~~\langle X_i\, X_j \rangle = \sum_{x_i, x_j} x_i \,x_j~ p(x_i,x_j) = \sum_{x_i, x_j} x_i\, x_j~ p(x_i)\,p(x_j) = \langle X_i \rangle\, \langle X_j \rangle, $$ где суммы идут по двум значениям $0,1$ каждой случайной величины. Вычислим теперь среднее квадрата частоты: $$ N^2\langle P^2 \rangle = \langle (X_1+...+X_N)^2 \rangle = \sum_i \langle X^2_i \rangle+ 2\sum_{i\lt j} \langle X_i X_j \rangle = \sum_i \langle X^2_i \rangle+ 2\sum_{i\lt j} \langle X_i \rangle \,\langle X_j \rangle = N p_A + N\,(N-1)\,p^2_A, $$ где учтено, что в первой сумме $N$ одинаковых слагаемых, а во второй - $N(N-1)/2$. Теперь по формуле $D=\langle P^2\rangle - P^2_\text{ср}$ несложно найти дисперсию $D=p_A(1-p_A)/N$.
Условная независимость
Два события $X,Y$ называют независимыми при условии, что происходит событие $Z$, если: $$ P(Z,\,Y\to X) = P(Z\to X),~~~~~~~~~~~~P(Z,\,X \to Y) = P(Z\to Y). $$ Условная независимость похожа на безусловную, в том смысле, что вероятность наступления $X$ не зависит от того, было ли событие $Y$ и наоборот. Но при этом эти вероятности зависят от третьего события $Z$.
Несложно проверить, что из этого определения следует соотношение $P(X,Y,Z)\,P(Z) = P(X,Z)\,P(Y,Z)$, которое позволяет факторизовать совместную условную вероятность для условно независимых $X,Y$: $$ P(Z\to X,\,Y) = P(Z\to X)\,P(Z\to Y). $$ Поэтому независимость $X,Y$ при условии $Z$ обозначают следующим образом: $X\Prep Y\mid Z$.
В общем случае для совместной вероятности трёх произвольных событий $X,Y,Z$ выполняется цепное правило: $P(X,Y,Z)=P(Z)\, P(Z\to X) \,P(Z,X\to Y).$ При наличии условной независимости $X\Prep Y\mid Z$ последний множитель заменяется на более простой: $$ P(X,Y,Z)=P(Z)\,P(Z\to X)\,P(Z\to Y). $$ Ситуации в которых $X_1\Prep X_2\Prep ...\Prep X_n\mid Z$ играют важную роль в машинном обучении. Например, $Z$ может быть фактом наличия болезни, а $X_i$ - условно независимыми её симптомами.
✒ Стоит проверить, что если $X,Y$ условно независимы и $X'$ является подмножеством $X$, а $Y'$ - подмножеством $Y$, то условно независимыми будут также и $X',Y'$: $$ X\Prep Y\mid Z,~~~~~X'\subseteq X,~~~~Y'\subseteq Y~~~~~~~\Rightarrow~~~~~~~X'\Prep Y'\mid Z $$ Напомним, что если $P(X'\to X)=1$, то $X' \subseteq X$ и $P(X',X)=P(X')$.
☝ Подчеркнём, что из парной независимости $X \Prep Y$ не следует
условная независимость для $X \Prep Y \mid Z$ и наоборот - условная независимость, вообще говоря,
не означает безусловной парной независимости.
Приведём два примера.
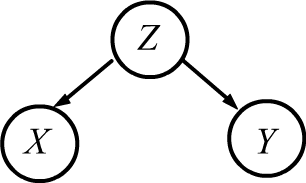 ◊ Когда $X:$ "продаёся много мороженного", тогда происходит $Y$: "несчастные случаи на воде"
и $P(X,Y)\neq P(X)P(Y)$. Но связно это с тем, что есть третья "управляющая переменная" - $Z$: "на улице жарко",
поэтому много и покупают мороженного, и купаются в водоёме.
◊ Когда $X:$ "продаёся много мороженного", тогда происходит $Y$: "несчастные случаи на воде"
и $P(X,Y)\neq P(X)P(Y)$. Но связно это с тем, что есть третья "управляющая переменная" - $Z$: "на улице жарко",
поэтому много и покупают мороженного, и купаются в водоёме.
В этом случае, скорее всего $X\Prep Y\mid Z$, но $X \NoPrep Y$ и
совместная вероятность равна:
$$
P(X,Y,Z)~=~P(Z)\,P(Z\to X,Y)~=~P(Z)\,P(Z\to X)\,P(Z\to Y),
$$
где первое равенство - это определение условной вероятности, а во втором учтено $X\Prep Y\mid Z$.
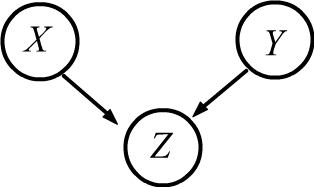 ◊ Пусть бросают два игральных кубика. Значение их очков $X,Y$ независимы $X\Prep Y$.
Однако, если есть информация $Z$: "сумма очков делится на 6",
то события не являются условно независимыми. $Z$ реализуется когда
$\{(X,\,Y)\} = \{(1,\,5);\, (5,\,1);\, (2,\,4);\, (4,\,2);\, (3,\,3);\, (6,\,6)\}$,
поэтому $P(Z\to X=3,Y=3)=1/6$. В тоже время $P(Z\to X=3)=P(Z\to Y=3)~=~1/6$,
поэтому условной независимости нет: $1/6 \neq (1/6)(1/6)$.
◊ Пусть бросают два игральных кубика. Значение их очков $X,Y$ независимы $X\Prep Y$.
Однако, если есть информация $Z$: "сумма очков делится на 6",
то события не являются условно независимыми. $Z$ реализуется когда
$\{(X,\,Y)\} = \{(1,\,5);\, (5,\,1);\, (2,\,4);\, (4,\,2);\, (3,\,3);\, (6,\,6)\}$,
поэтому $P(Z\to X=3,Y=3)=1/6$. В тоже время $P(Z\to X=3)=P(Z\to Y=3)~=~1/6$,
поэтому условной независимости нет: $1/6 \neq (1/6)(1/6)$.
Диаграммы, приведенные справа, называются байесовскими сетями. Они играют важную роль в машинном обучении и в теории вероятностного логического вывода. Вероятностное рассуждение(reasoning) или вывод (inference) сотоит в построении вероятностной модели $P(X_1,...,X_n)$ для $n$ переменных (случайных величин). Обычно известно некоторое подмножество переменных. На основании этой информации требуется выяснить вероятности других величин, например: $P(X_1,X_2\to X_3)$. Основная проблема состоит в построении вероятностной модели. Даже для бинарных случайных величин (=событий) требуется задание $2^n-1$ чисел. При больших $n$ это проблематично в вычислительном плане и не реалистично в эмпирическом. В этой ситуации на помощь приходят условные независимости между величинами, которые позволяют разбить совместную вероятность на произведение более простых.