ML: : Предсказание букв
Введение
Рассмотрим пример прогнозирования очередной буквы текста при помощи рекуррентной нейронной сети. Исходный код можно найти в нотбуке NN_RNN_Torch_Chars.ipynb
Формирование данных
В качестве небольшого полигона будем использовать "Сказка о царе Салтане". Алфавит CHARS возьмём фиксированным и включим в него конец строки '\n' (стихи):
CHARS = " .абвгдежзийклмнопрстуфхцчшщъыьэюя\n" # алфавит
charID = { c:i for i,c in enumerate(CHARS) } # буква в номер
Загрузим текст из файла, переведём в нижний регистр, вычистим двойные пробелы и т.п.:
import re
with open("saltan.txt", "r", encoding='utf-8-sig') as file:
text = file.read()
text = text.lower().replace('ё','e')
text = ''.join( [c if c in CHARS else ' ' for c in text] )
text = re.sub(' +', ' ', text).replace(' .', '.')
text = re.sub('\n\s+', '\n', text)
Для формирования обучающих данных, скользим по тексту окном длиной LENGTH с шагом STEP букв. Номера букв, попавших в окно, помещаем в X_dat. В целевой массив Y_dat помещаем буквы, сдвинутые на одну вперёд:
LENGTH, STEP = 25, 25 # длина истории, смещение по тексту
textID = [ charID[c] for c in text ] # текст - список индексов (номера в CHARS)
num_seq = int((len(textID)-LENGTH)/STEP)-1 # число последовательностей
X_dat = torch.empty (num_seq, LENGTH, dtype=torch.long)
Y_dat = torch.empty (num_seq, LENGTH, dtype=torch.long)
for i in range(num_seq):
X_dat[i] = torch.tensor(textID[i*STEP: i*STEP+LENGTH], dtype=torch.long)
Y_dat[i] = torch.tensor(textID[i*STEP+1: i*STEP+LENGTH+1], dtype=torch.long)
Шаг STEP выбран равным ширине окна LENGTH, чтобы проверочные данные
после перемешивания не пересеклись с тренировочными (см. следующий раздел).
Перемешаем данные и разобьём их на тренировочное (X_trn, Y_trn)
и проверочное (X_val, Y_val) множества:
idx = torch.randperm( len(X_dat) ) # перемешанный список индексов X_dat, Y_dat = X_dat[idx], Y_dat[idx] num_trn = int(0.75*len(X_dat)) # доля тренировочных данных X_trn, Y_trn = X_dat[:num_trn], Y_dat[:num_trn] X_val, Y_val = X_dat[num_trn:], Y_dat[num_trn:]
Стратегия обучения
В принципе, можно обучать сеть предсказывать Y_trn по входу X_trn, задействуя все выходы рекуррентного слоя. Однако, мы поступим иначе. Введём гиперпараметр NUM, который меньше длины последовательности LENGTH. По первым LENGTH - NUM ячейкам сеть будет накапливать скрытое состояние (историю). Ошибки же предсказания будут вычисляться только по последним NUM ячейкам. Использование значений NUM > 1 целесообразно для уменьшения затухания градиента при его обратном распространении.
Ниже нарисована двухслойная RNN-сеть. На входы ячеек первого слоя поступает текст "вечерко" На самом деле одновременно в обучении участвует не один, а B примеров длины L (батч). Поэтому на входе сети находится тензор формы (B,L), содержащий номера букв. Он проходит через слой Embedding и каждая буква превращается в E-мерный вектор, т.е. получается тензор (B,L,E):
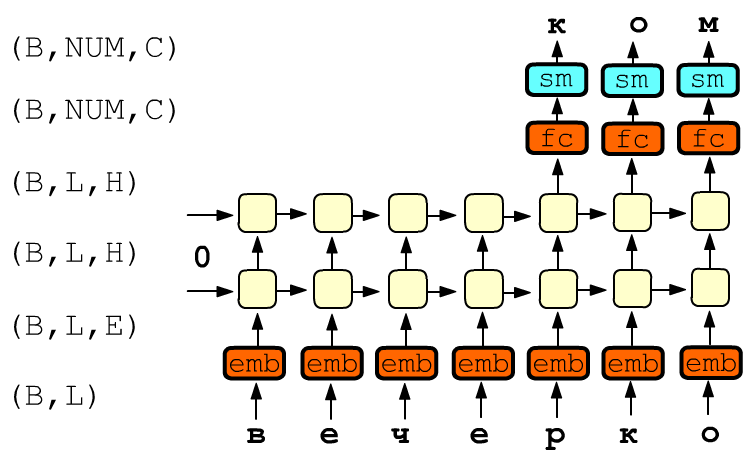
Выход последнего RNN-слоя имеет размерность (B,L,H), где H - размерность скрытого состояния. Для вычисления ошибки берутся только последние NUM ячеек. Поэтому тензор (B,NUM,H), при помощи полносвязного слоя fc (fully connected) с матрицей формы (H,C), преобразуется в тензор (B,NUM,С), где С-число букв в алфавите (число классов). После пропуска этого тензора через функцию софтмакса sm, для каждого примера B и выхода NUM получается С чисел, которые интерпретируются как вероятности той или иной буквы (сумма чисел после sm равна единице). Ошибка предсказания вычисляется как средняя CrossEntropyLoss по всем выходам NUM и примерам B.
Модель
В конструкторе модели создадим слой эмбединга, стопку из NUM_LAYERS рекуррентных слоёв GRU, выходной полносвязный слой Linear и Dropout слой, который с вероятность DROP обнуляет компоненты тензора перед fc:
class Model(nn.Module):
def __init__(self, C, E, H, LAYERS = 1, DROP = 0):
super(Model, self).__init__()
self.emb = nn.Embedding(C, E, scale_grad_by_freq=True)
self.rnn = nn.GRU (E, H, num_layers=LAYERS, batch_first=True, dropout=0.2)
self.drop = nn.Dropout(DROP)
self.fc = nn.Linear (H*LAYERS, C)
Обратим внимание на параметр scale_grad_by_freq при создании слоя Embedding. Буквы в тексте имеют существенно различную вероятность. Поэтому во время обучения более частые буквы будут интенсивнее менять компоненты своих векторов, чем более редкие. При параметре scale_grad_by_freq = True по текущему батчу вычисляются вероятности букв и векторы более редких букв оптимизатор сдвигает сильнее.
Метод прямого распространения forward определяет последовательность вычислений. Справа в комментариях приведены формы получаемых тензоров.
. def forward(self, x, h0=None, NUM=1): # (B,L), (1,B,H)
x = self.emb ( x ) # (B,L,E)
yr, hr = self.rnn ( x, h0 ) # (B,L,H), (1,B,H)
y = yr[:, -NUM:, :] # (B,NUM,H) последние выходы
y = self.drop(y)
y = self.fc(y) # (B,NUM,C)
return y.transpose(1,2), hr # (B,C,NUM), (LAYERS,B,H)
В нашей стратегии обучения, матрица полносвязного слоя fc сворачивается
не со всем выходным тензором (B,L,H), а только с его срезом
(B,NUM,H).
Кроме ускорения, это может приводить к существенной экономии памяти при большом размере словаря
(когда вместо букв работают со словами). Пусть, к примеру, в батче B=100 примеров,
размерность скрытого состояния H=500
и в словаре C=100'000 слов.
Тогда тензор всех выходов RNN-слоя
имеет 100*500*L элементов, а тензор после полносвязного слоя
в 200 раз его больше: 100*100000*L. При длинных последовательностях L,
такой тензор может даже не поместиться в память графической карты. Поэтому сворачивать
все выходы RNN слоя с полносвязным выходным слоем fc не целесообразно.
Создание экземпляра модели стандартно. При наличии графической карты gpu, параметры модели сразу отправляются в её память. Список losses нам понадобится в дальнейше для визуализации истории ошибок обучения.
E_DIM, H_DIM, NUM_LAYERS, DROP = 10, 250, 1, 0
model = Model(len(CHARS), E_DIM, H_DIM) # экземпляр сети
gpu = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
cpu = torch.device("cpu")
model.to(gpu)
losses = [] # история ошибок для графика
Веса классов и функция ошибки
Ещё один способ борьбы с перекосом вероятностей классов (букв), является использование весов степени важности ошибки данной буквы. Если все веса одинаковые, то сеть стремится лучше предсказывать частые буквы, чем более редкие. Чтобы снизить этот эффект, вычислим частоту каждой буквы weight, а затем возьмём её логарифм с обратным знаком.
weight = torch.zeros(len(CHARS), dtype=torch.float)
for c in textID:
weight[c] += 1
weight /= len(text)
weight = -weight.log_()
Приведём веса для 5 наиболее частых и 5 наиболее редких букв:
' ': 1.86 'о': 2.51 'е': 2.76 'а': 2.72 'и': 2.98
'ю': 5.49 'щ': 6.44 'э': 7.49 'ъ': 7.49 'ф': 8.95
Использование логарифма делает увеличение веса редких букв более мягким
по сравнению, например, с обратной вероятностью.
Нормировать веса не обязательно, так как функция ошибки это делает сама.
CE_loss = nn.CrossEntropyLoss(weight.to(gpu))
Обучение
Функция обучения на одну эпоху имеет вид:
def fit(model, X,Y, batch_size=64, NUM=1, train=True):
model.train(train) # важно для Dropout
sumL, iters = 0, int(len(X)/batch_size)
tm1 = tm()
for it in range(iters): # примеры разбиты на пачки
xb = X[it*batch_size: (it+1)*batch_size].to(gpu) # (B,L)
yb = Y[it*batch_size: (it+1)*batch_size].to(gpu) # (B,L)
y, _ = model(xb, NUM=NUM)
L = CE_loss(y, yb[:, -NUM:])
sumL += L.detach().item()
if train: # в режиме обучения
optimizer.zero_grad() # обнуляем градиенты
L.backward() # вычисляем градиенты
optimizer.step() # подправляем параметры
if tm() - tm1 > 1 or it+1==iters:
print('\r', f"{100*(it+1)/iters:.0f}% loss: {sumL/(it+1):.4f}", end='')
tm1 = tm()
return sumL/iters
Запуск обучения:
from IPython.display import clear_output
import matplotlib.pyplot as plt
for epoch in range(100):
optimizer = torch.optim.Adam(model.parameters(), lr=0.001, betas=(0.9, 0.999))
idx = torch.randperm( len(X_trn) ) # перемешанный список индексов
X_trn = X_trn[idx]
Y_trn = Y_trn[idx]
L_trn, A_trn = fit(model, X_trn, Y_trn, 256, NUM = 25, train=True )
L_val, A_val = fit(model, X_val, Y_val, 256, NUM = 25, train=False)
losses.append([L_trn, L_val])
clear_output(wait=True)
plt.figure(figsize=(16,4)); plt.plot(losses); plt.legend(['trn', 'val']); plt.show()
print('\r', f'epoch: {epoch:d}/{len(losses)-1} {tm()-beg:.2f}s ',
f'loss: trn={L_trn:.4f} val={L_val:.4f} ' )
One-hot vs Embedding
Так как букв в словаре немного, можно было бы убрать слой Embedding, выполнив one-hot кодирование. Для этого достаточно положить E_DIM=len(CHARS) и заменить в функции forward строку x = self.emb ( x ) на:
B, L, C = len(x), x.size(1), self.fc.size(-1) x = torch.zeros(B,L,C).scatter_(2, x.unsqueeze(2), 1.) # (B,L,C) x = x.transpose(0,1).contiguous() # (L,B,C)Так как x имеет форму (B,L), сначала создаётся тензор (B,L,C), заполненный нулями. Метод x.unsqueeze(2) это изменение формы тензора: (B,L) -> (B,L,1). Метод scatter_ ставит в последнем индексе тензора единицы в позиции, соответствующей значению x. Псевдокод для этого метода: self[i,j, x[i,j,k]] = 1. Например:
L, C = 3, 4 x = torch.tensor([ [1,0,1], [0,2,3] ], dtype=torch.long) x = torch.zeros(len(x), 3, 4).scatter_(2, x.unsqueeze(2), 1.) # (B,L,C) [[[0., 1., 0., 0.], [1., 0., 0., 0.], [0., 1., 0., 0.]], [[1., 0., 0., 0.], [0., 0., 1., 0.], [0., 0., 0., 1.]]])