ML: Attention - GPT Model
Introduction
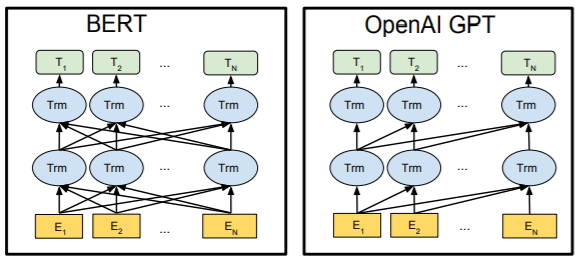
After the Transformer architecture, based on the attention mechanism, demonstrated its effectiveness, its individual components began to evolve independently. Initially, OpenAI developed a network called Generative Pre-trained Transformer (GPT), which used a modified Transformer decoder. Later, Google created Bidirectional Encoder Representations from Transformers (BERT), using the encoder part.
In addition to the Transformer architecture, the new models share a common training strategy
on a large corpus of unlabeled text.
GPT predicts the next word in a sequence, while BERT
predicts the "masked" words within a sentence.
As a result of such training, a language model is formed,
which captures grammar, semantics, and even certain knowledge.
After this pre-training stage, the model’s parameters are fine-tuned
for a specific task using labeled data.
GPT
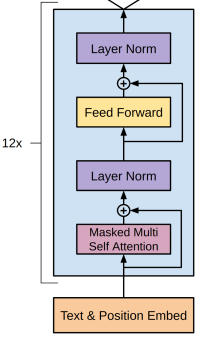The GPT network is a Transformer decoder
from which the second attention block is removed, making it similar to an encoder.
However, the key difference from the encoder lies in the use of masked self-attention.
Since the model is trained to predict the next word during pretraining,
each word in the input sequence can "see" only the words preceding it, but not the ones that follow.
Therefore, a mask is added to the self-attention weights,
where the elements above the diagonal are set to negative infinity.
An unlabeled sequence of words $w_1,...,w_n$ is vectorized using an embedding matrix $\mathbf{W}_e$, and positional embeddings $\mathbf{W}_p$ are added to represent word positions in the sequence. As a result, a matrix $\mathbf{h}_0:~(N,B,E)$ is obtained, which passes through the decoder blocks 12 times (each with different parameters). The decoder output (of the same shape) is multiplied by the transposed embedding matrix $\mathbf{W}_e$, and the word probabilities for the sequence shifted one position to the right $w_2,...,w_{n+1}$ are computed using the softmax function: $$ \mathbf{h}_k = \text{Decoder}(\mathbf{h}_{k-1}),~~~~~~~~~~~P(w_{n+1}) = \text{softmax}(\mathbf{h}_{12}\cdot\mathbf{W}^\top_e). $$
The model was trained on the BooksCorpus dataset, where it achieved a very low perplexity of 18.4.
GPT: Fine-tuning
During fine-tuning, the output vector of the last word in the input sequence $\mathbf{h}^n_{12}$ is used. This vector is multiplied by a trainable matrix $\mathbf{W}_c$, and the subsequent softmax function produces probabilities for the target task. For example, suppose there is a sequence of tokens $w_1,...,w_n$ that belongs to class $c$. Then the conditional probability of belonging to this class is: $$ P(c|w_1...w_n) = \text{softmax}(\mathbf{h}^n_{12}\cdot \mathbf{W}_c). $$ Technically, the word sequence is also surrounded by special tokens <s> - start and <e> - end:
In more structured tasks, the input data is packed into a single sequence using additional delimiter tokens. For example, in the Natural Language Inference task, a delimiter token <$> - delim is placed between the premise and the hypothesis. The predicted class (entailment, contradiction, neutral) is determined, as before, from the output of the last token:
In the sentence similarity task with two texts Text1 and Text2, the order of the texts does not matter. Therefore, they are arranged twice - once as (Text1, Text2) and once as (Text2, Text1). The outputs of the last tokens are summed and passed again through a linear classification layer:
Finally, in question-answering tasks, a context document $d$, a question $q$, and a set of possible answers $a_i$ are provided. The context and the question are concatenated, and between them and each answer a delimiter <$> is inserted: $(d,q$ <$> $a_i)$. Each such sequence for every answer is passed through the decoder, linear layer, and softmax. The answer with the maximum response is then selected.
References
Articles
- 2014: Sutskever I, et al. "Sequence to Sequence Learning with Neural Networks"
- invention of the Encoder-Decoder architecture for RNNs. - 2014: Bahdanau D., et al. "Neural Machine Translation by Jointly Learning to Align and Translate
- introduction of the Attention mechanism for the Encoder-Decoder architecture. - 2017: Vaswani A., et al. "Attention is All You Need"
- elimination of recurrent networks, introduction of the Transformer architecture (Google Brain). - 2018: Devlin J., et al. "BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding"
- use of the Transformer encoder and a large amount of unlabeled data for pretraining (Google AI Language). - 2018: Radford A., et al. "Improving Language Understanding by Generative Pre-Training"
- GPT-1 model (OpenAI). - 2019: Radford A., et al. "Language Models are Unsupervised Multitask Learners"
- GPT-1 model (OpenAI). - 2020: Radford A., et al. "Language Models are Few-Shot Learners"
- GPT-3 model - the third generation of GPT, an excellent text generator (OpenAI).
Additional materials
