RL: Q-обучение, непрерывные состояния
Введение
В этом документе мы продолжаем изучать алгоритмы обучения с подкреплением, основанные на $Q$-функции (Q-learning). Как и ранее, будем считать, что действия агента дискретны, однако теперь рассмотрим случай непрерывных состояний, который более типичен для большинства сред, рассматриваемых в обучении с подкреплением.
Сначала мы сведём непрерывную задачу к дискретной на примере MountainCar-v0. Затем перейдём к методу DQN, который использует нейронную сеть для аппроксимации Q-функции. После этого будут приведены две его простые модификации под названиями Double DQN и Dueling DQN.
Дискретизация состояния
При небольшой размерности вектора состояния можно провести его дискретизацию, разбив каждую компоненту на интервалы. Тем самым мы снова переходим к дискретному множеству состояний. В задаче MountainCar-v0 состояние определяется двумя вещественными числами $s=\{x,v\}$ (положение и скорость машинки). Их диапазоны изменения $x \in [-1.2,\, 0.6]$ и $v\in [-0.07,\,0.07]$ разобьём на 101 интервал, что приводит к 101*101 = 10201 состояниям:
bins = (101, 101) # число интервалов по каждой оси
low = np.array([-1.2, -0.07]) # минимальные значения наблюдения
high = np.array([ 0.6, 0.07]) # минимальные значения наблюдения
bin = (high-low)/bins # ширины интервалов
def index(state): # вещественный state в пару индексов
indx = (state - low) / bin
indx = indx.clip(np.zeros_like(low), np.array(bins)-1)
return tuple( indx.astype(int) )
actions = [0,2] # используемые действия
Табличное представление Q-функции и функция политики выглядят следующим образом:
Q = np.zeros( bins + (len(actions),) ) # (101, 101, 2)
def policy(self, state):
if np.random.random() < epsilon: # random action
return np.random.randint(len(actions))
s = index(state) # (ix, iv) - кортеж целых чисел
return np.argmax(Q[s]) # Q[(ix,iv)] это Q[ix, iv, :]
Функция argmax возвращает номер действия для которого Q максимальна.
При этом Q[s] - это строка матрицы Q[s,a] значений Q для каждого действия.
Ниже приведены кривые обучения при различных гиперпараметрах. Отметим, что для этой задачи эпсилон-распад не нужен, а при $\gamma = 1$ обучение становится неустойчивым, но его можно выбрать сколь угодно близко к единице:
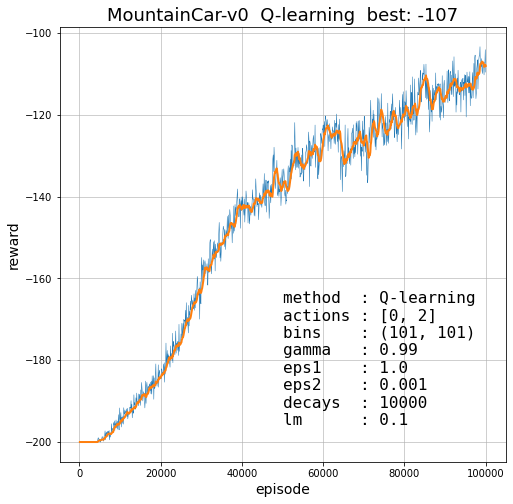
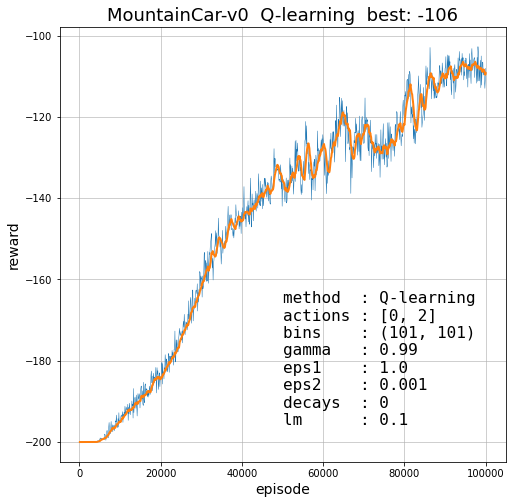
Проблемы дискретизации
При дискретизации возникает возникает две проблемы. Во первых, если число компонент вектора состояния велико, размерность матрицы $Q$ становится очень большой, что может приводить к медленному обучению и большим расходам памяти. Во вторых, для непрерывных состояний, функция политики, обычно, имеет достаточно гладкие разделяющие границы между областями различных действий.
Ниже на первом рисунке приведены действия $a=\arg\max Q$ для матрицы в задаче MountainCar. Синие точки - action=0, красные - action = 2. Серая область - состояния в которые система при обучении ни разу не попала. Вертикальные линии соответствуют минимуму ландшафта и целевой координате. Риски на горизонтальной линии - область откуда машина равновероятно стартует (с нулевой скоростью).
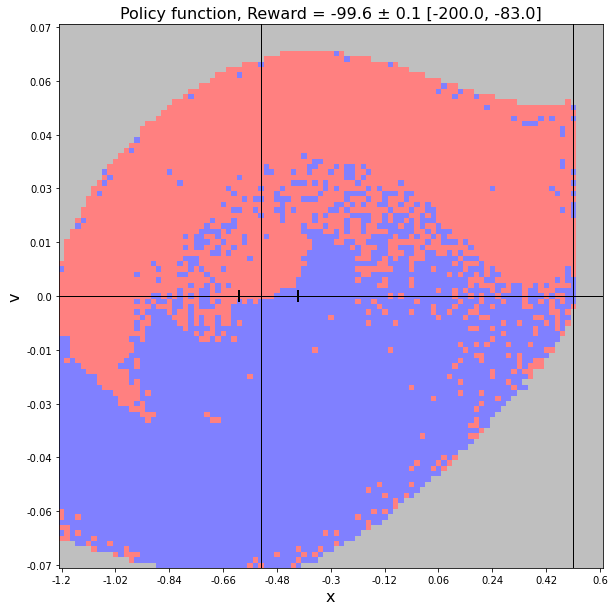
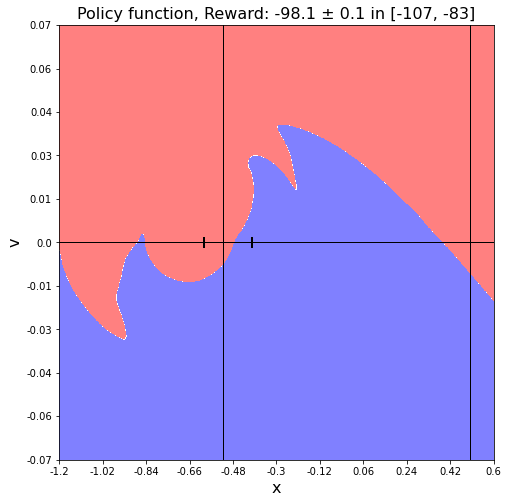
На втором рисунке приведена "точная" функция политики для этой задачи. Хотя разделяющая поверхность между действиями причудливо изгибается, она вполне гладка, а области действий непрерывны. Однако, Q-обучение не учитывает соседних значений в пространстве состояний, поэтому она имеет негладкую структуру, что видно из первого рисунка.
Один из способов решения второй проблемы - это периодическое усреднение матрицы, что приводит к её сглаживанию. На библиотеке PyTorch это можно сделать, например, при помощи слоя пулинга с усреднением:
pool = nn.AvgPool2d(3, stride=1, padding = 1, count_include_pad=False) Q = pool(torch.tensor(Q).permute(2,0,1)).permute(1,2,0).numpy()Подобная стратегия в задаче MountainCar позволяет получить среднюю награду порядка -100.
Отметим, что во всех методах, основанных на Q-обучении, следует следить за средним значением $Q$-функции, так как иногда происходит её неконтролированный рост (расхождение обучения). Разработан ряд методов по борьбе с этим эффектом. Простейший - приводить среднюю награду по состояниям к интервалу $[-1,+1]$. Важно также следить за дисперсией $Q$, так как она может вырождаться в константу $Q=\mathrm{const}$.
Метод DQN
Для непрерывных состояний естественно аппроксимировать функцию полезности состояний нейронной сетью $Q(s,a;\,\theta)$ с параметрами $\theta$. При этом решаются обе упомянутые выше проблемы (размерность и зашумлённость). Обучать сеть следует таким образом, чтобы Q-функция удовлетворяла уравнению Беллмана.
Первым и по-прежнему популярным методом является Deep Q-Network = DQN (2015). DQN произвёл революцию в RL, когда с его помощью DeepMind в 2013г. удалось обучить агента побеждать в играх Atari по видео изображению. Метод имеет две ключевые идеи: 1) хранение предыдущей истории состояний-действий и 2) использование двух нейронных сетей (одинаковой архитектуры) для текущей Q-функции и "целевой" (полученной на предыдущих этапах обучения).В алгоритме DQN агент, как и в Q-обучении, совершает "оптимальное" действие $a_t = \arg\max_a Q(s_t,a;\,\theta_t)$, возможно, с не жадной $\epsilon$-стратегией, получает от среды новое состояние и награду $s_{t+1},~r_{t+1}$. В конечной памяти сохраняются четвёрки соседних значений $(s,\,a,\,s',\,r') = (s_t,\,a_t,\,s_{t+1},\,r_{t+1})$ по достаточно большому числу эпизодов. Фактически это не устареваемые данные характеризующее модель среды. Тем не менее память должна быть конечной, чтобы "забывать" области пространства состояний и действий вдали от оптимальной стратегии.
При обучении, после каждого временного шага, из памяти случайным образом извлекается батч (наборы четвёрок). Случайная выборка решает проблему корреляций последовательных во времени состояний, которые обычно не сильно отличаются друг от друга. Именно эта корреляция мешала глубокому обучению до работы DeepMind.
При помощи батча формируется функция ошибки равная квадратам отклонений примеров от уравнения Беллмана с жадной стратегией выбора действия ($B$ - размер батча): $$ L(\theta) = \frac{1}{B}\sum^B_{i=1} \Bigr[ r'_i + \gamma\,\max_a Q(s'_i,a; \bar{\theta}) - Q(s_i,a_i; \theta) \Bigr]^2. $$ В слагаемом $\max_a Q(s',a; \bar{\theta})$ стоят фиксированные параметры $\bar{\theta}$ целевой сети, полученные на предыдущих итерациях обучения . После нескольких циклов обучения $\bar{\theta}$ заменяются на текущие значения. Таким образом, основная сеть оценивает ценность текущего состояния и действия, а целевая сеть оценивает ценность следующего состояния и действия. Иногда целевая сеть "замораживается" (не меняется) на протяжении нескольких десятков тысяч итераций обучения.Хотя в некоторых задачах эффективнее и жёсткое (частое) обновление Обе сети имеют одинаковую архитектуру и вначале их веса инициализируются различными случайными значениями. Использование целевой (старой) сети для действий и вычисления max делают обучения более устойчивым ("не стоит оптимизировать на ходу быстро едущую машину").
Вместо MSE-ошибки иногда лучше работает ошибка huber (HuberLoss) в которой используется парабола $x^2$ в окрестности нуля и $|x|$ при больших отклонениях (с их гладкой сшивкой). В этом случае уменьшается вес больших выбросов от уравнения Беллмана, которые возможно случайны.
MountainCar DQN
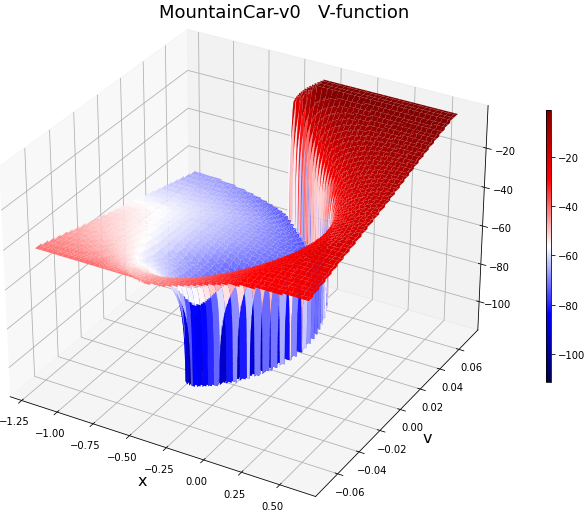
В задаче MountainCar функция политики достаточно простая, чего нельзя сказать о Q и V функциях. Справа на рисунке приведена "точная" V-функция. Эта поверхность имеет спиральную форму с резкиими обрывами вниз. Область V-функции с максимальными значениями находится в верхнем правом уголу (тёмно-красный цвет). Она соответствует целевой области в пространстве состояний $\{x,v\}$. Аналогичную сложную форму имеет Q-функция. Поэтому эта задача достаточно сложная и на числе нейронов экономить не стоит.
В методе DQN много гиперпараметров. Прежде всего - это архитектура нейронной сети. В этой задаче она должна иметь два входа ($x$,$v$) и три выхода (значения $Q$ для каждого действия). Между ними мы будем использовать два слоя. Следующие гиперпараметры - это фактор дисконтирования gamma и параметры $\epsilon$-жадной стратегии: начальное eps1, конечное eps2 и число эпизодов decays за которые должен произойти экспоненциальный распад, после которого полагается $\epsilon=0$.
Параметр capacity - это ёмкость памяти batch число примеров в батче, которые извлекаются из памяти. Обучение происходит после каждого временного шага (не после эпизода!). Параметр update означает частоту (во временных шагах) копирования новой сети в старую (целевую). Наконец, как обычно, есть функция ошибки, скорость обучения lm и алгоритм оптимизации (SGD, Adam и т.п.).
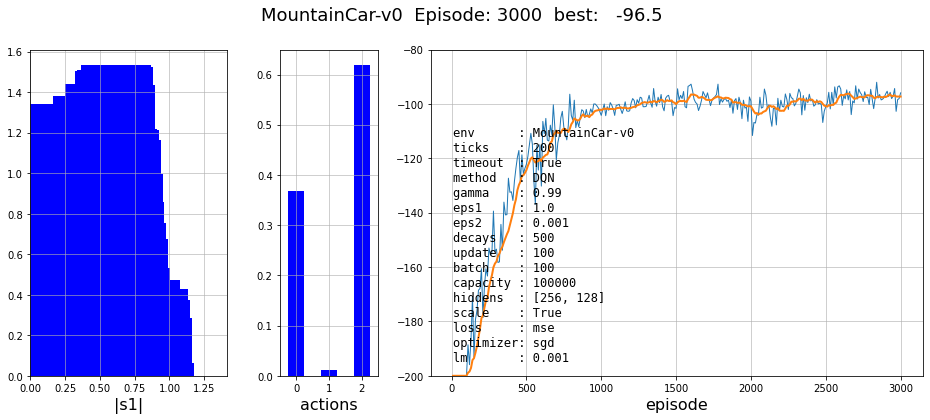
Ниже приведен пример кривой обучения за 5000 эпизодов. На первом графике нарисована гистограмма распределения длин состояния $s'$. Вначале обучения она прижата влево, т.е. большинство примеров в памяти соответствуют малым скоростям и координатам (в окрестности минимума). Под конец обучения, эта гистограмма размывается. На второй гистограмме - приведено распределение в памяти различных действий. Как видно, под конец обучения метод исключает неэффективное в этой задаче действие $a=1$ (ничего не делаем).
Проблема нестабильности
Нестабильность обучения - типичная проблема многих методов в задачах RL. По борьбе с ней можно дать следующие рекомендации:- Реже обновлять целевую (старую) сеть, что называется мягким обновлением. Если целевую сеть менять сразу или даже после каждого батча - это называется жестким обновлением.
- Увеличивать размер памяти. Это очень важный фактор. Кроме этого, нужно следить за "разнообразием" примеров в памяти, подобно гистограммам приведенным выше.
- Следить за скоростью обучения (она не должна быть слишком большой) и использовать адаптивные алгоритмы обучения типа Adam. Хотя для сетей с простой архитектурой обычный стохастический градиент SGD справляется иногда лучше.
- Обычно не стоит экономить на числе нейронов в скрытых слоях, так как поверхность $Q(s,a)$ может быть очень сложной. Лучше их уменьшить после подбора параметров дающих устойчивое обучение.
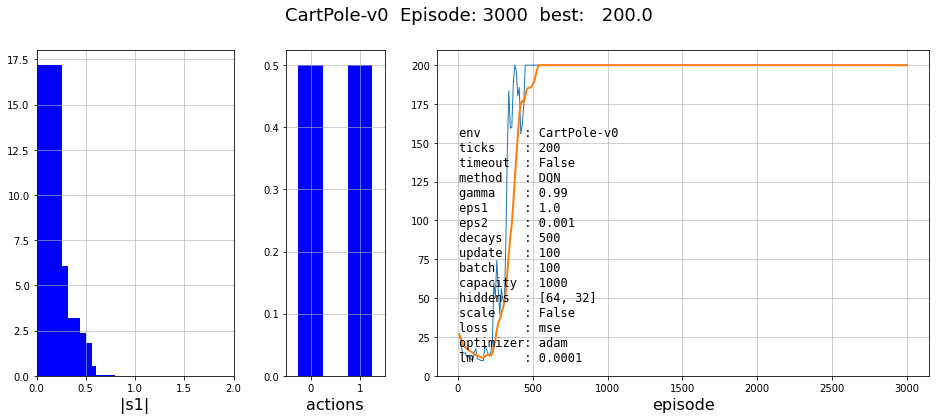
- Как обычно, вход нейронной сети следует масштабировать на интервал [-1...1]. Хотя надо быть осторожным, так как возвращаемые средой минимальные и максимальные значения не всегда соответствуют реальности. Так, в задаче CartPole-v0 скорости декларируются в бесконечных диапазонах, что очевидно не соответствует реальной работе со стержнем. В этом случае, нужно либо отказаться от масштабирования, или задать их руками (например, проведя статистический анализ средних значений и дисперсий по каждой компоненте).
Детали реализации
Приведём код реализации алгоритма DQN. Прежде всего создадим класс памяти для хранения примеров модели среды:
class Memory:
def __init__(self, capacity, nS):
self.capacity = capacity # вместимость памяти
self.count = 0 # число помещённых примеров
self.S0 = torch.empty( (capacity, nS), dtype=torch.float32)
self.S1 = torch.empty( (capacity, nS), dtype=torch.float32)
self.A0 = torch.empty( (capacity, 1), dtype=torch.int64)
self.R1 = torch.empty( (capacity, 1), dtype=torch.float32)
self.Dn = torch.empty( (capacity, 1), dtype=torch.float32)
def add(self, s0, a0, s1, r1, done):
""" Add to memory (s0,a0,s1,r1) """
idx = self.count % self.capacity
self.S0[idx] = torch.tensor(s0, dtype=torch.float32)
self.S1[idx] = torch.tensor(s1, dtype=torch.float32)
self.A0[idx] = a0; self.R1[idx] = r1; self.Dn[idx] = done
self.count += 1
def get(self, count):
""" Return count of examples for (s0,a0,s1,r1) """
high = min(self.count, self.capacity)
num = min(count, high)
ids = torch.randint(high = high, size = (num,) )
return self.S0[ids],self.A0[ids],self.S1[ids],self.R1[ids],self.Dn[ids]
Метод обучения будет находиться в классе DQN. Параметры метода удобно собрать в словарь,
значения которого в конструкторе зададим по умолчанию:
class DQN:
""" DQN method for for discrete actions """
def __init__(self, env):
self.env = env # среда с которой мы работаем
self.low = env.observation_space.low # минимальные значения сост.
self.high = env.observation_space.high # максимальные значения сост.
self.nA = self.env.action_space.n # число действий
self.nS = self.env.observation_space.shape[0] # число компонент сост.
self.params = { # параметры по умолчанию
'ticks' : 200, # длительность эпизода
'timeout' : True, # истечение времени терминальное?
'gamma' : 0.99, # фактор дисконтирования
'eps1' : 1.0, # начальное значение epsilon
'eps2' : 0.001, # конечное значение epsilon
'decays' : 500, # число эпизодов на его распад eps1->eps2
'update' : 100, # обновление целевой модели (в шагах)
'batch' : 100, # размер батча
'capacity' : 100000, # ёмкость памяти
'hiddens' : [256,128], # нейрронов в скрытых слоях
'scale' : True, # масштабировать ли состояние к [-1...1]
'lm' : 0.001, # скорость обучения
}
Функция create_model класса DQN создаёт нейронную сеть по списку нейронов в скрытых слоях.
def create_model(self, sizes, hidden=nn.ReLU, output=nn.Identity):
layers = []
for i in range(len(sizes)-1):
activation = hidden if i < len(sizes)-2 else output
layers += [ nn.Linear(sizes[i], sizes[i+1]), activation() ]
return nn.Sequential(*layers)
Эта функция вызывается в методе инициализации init,
где создаётся две сети - основная (model) и целевая (target).
Кроме этого, задаётся функция ошибки и оптимизатор:
def init(self):
self.device =torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
sizes = [self.nS] + self.params['hiddens'] + [self.nA]
self.model = self.create_model(sizes).to(self.device) # текущая Q
self.target = self.create_model(sizes).to(self.device) # целевая Q
self.loss = nn.MSELoss()
self.optimizer = torch.optim.Adam(self.model.parameters(),
lr=self.params['lm'])
self.memo = Memory(self.params['capacity'], self.nS)
self.maxQ = torch.zeros( (self.params['batch'], ),
dtype=torch.float32).to(self.device)
self.epsilon = self.params['eps1']
self.decay_rate = np.exp(np.log(self.params['eps2']
/self.params['eps1'])/self.params['decays'])
Функция политики следует epsilon-жадной стратегии:
def policy(self, state):
""" Return action according to epsilon greedy strategy """
if np.random.random() < self.epsilon:
return np.random.randint(self.nA) # случайное
x = torch.tensor(state, dtype=torch.float32).to(self.device)
with torch.no_grad():
y = self.model(x).detach().cpu().numpy()
return np.argmax(y) # лучшее
Функция масштабирования приводит вход сети к интервалу [-1...1],
если определён соответствующий параметр:
def scale(self, obs):
""" to [-1...1] """
if self.params['scale']:
return -1. + 2.*(obs - self.low)/(self.high-self.low)
else:
return obs
Примеры модели среды сохраняются в функции запуска одного эпизода.
Она же копирует основную сеть в целевую (load_state_dict)
и запускает обучение после каждого временного шага:
def run_episode(self, ticks):
rew = 0 # общая награда
s0 = self.env.reset() # начальное состояние
s0 = self.scale (s0) # масштабируем его
a0 = self.policy(s0) # получаем действие
for t in range(1, ticks+1):
s1, r1, done, _ = self.env.step(a0) # совершаем действие
s1 = self.scale (s1)
a1 = self.policy(s1)
dn = done and (self.params['timeout'] or t < ticks)
self.memo.add( s0, a0, s1, r1, float(dn) )
if self.frame % self.params['update'] == 0:
self.target.load_state_dict( self.model.state_dict() )
if self.memo.count >= self.params['batch']:
self.learn_model()
rew += r1
self.frame += 1
if done:
break
s0, a0 = s1, a1
return rew
Кроме четвёрки $(s,a,s'r')$, сохраняется признак достижения терминального состояния.
Ценность такого состояния равна нулю, что будет учитываться при обучении.
Существует тонкость связанная с интерпретацией окончания эпизода
по истечению отведенного на него времени. Среда в этот момент может находиться
в состоянии которое не является терминальным и не имеет нулевой ценности.
В CartPole - если по концовке эпизода стержень продолжает стоять вертикально,
агент бы в будущем продолжал получать награды.
Для MountainCar, аналогично, если машинка не успела добраться до цели,
но находится с хорошей скоростью недалеко от него - это тоже по факту не терминальное состояние.
Однако польза от параметра timeout определяется задачей. В CartPole значение timeout=True стабилизирует обучение при достижении максимальной награды, а в MountainCar обучение вообще не происходит.
Собственно обучение модели выглядит следующим образом:
def learn_model(self):
""" Model Training """
s0, a0, s1, r1, dn = self.memo.get(self.params['batch'])
s0 = s0.to(self.device); s1 = s1.to(self.device); a0 = a0.to(self.device)
r1 = r1.to(self.device); dn = dn.to(self.device)
with torch.no_grad():
y = self.target(s1).detach()
self.maxQ, _ = torch.max(y, 1) # максимальное Q для s1
q1 = self.maxQ.view(-1,1)
yb = r1 + self.params['gamma']*q1*(1.-dn)
y = self.model(s0) # прямое распространение
y = y.gather(1, a0)
L = self.loss(y, yb)
self.optimizer.zero_grad() # обнулить градиенты
L.backward() # пересчитать их обратно
self.optimizer.step() # поменять параметры
Обратим внимание на функцию gather в каждой строчке матрицы
y выбирает значение из колонки с номером a0.
Запуск обучения совершает последний метод:
def learn(self, episodes = 100000, stat = 100):
""" Repeat episodes episodes times """
self.frame = 1
rews, mean = [], 0
for episode in range(1, episodes+1):
rew = self.run_episode( self.params['ticks'] )
rews.append( rew )
self.epsilon *= self.decay_rate # epsilon-распад
if self.epsilon < self.params['eps2']:
self.epsilon = 0.
if episode % stat == 0:
mean, std = np.mean(rews[-stat:]), np.std(rews[-stat:])
print(f"{episode:6d} rew: {mean:7.2f} ± {std/stat**0.5:4.2f}")
Этот код можно найти в файле DQN_simple.py. Можно также загрузить блокнот, в котором добавлена визуализация процесса обучения.
Double DQN
Считается, что в методе DQN агент переоценивает будущее вознаграждение. Чтобы исправить это, авторы алгоритма Double DQN (DDQN) предложили отделить выбор действия от оценки действия, поэтому они меняют минимизируемую ошибку следующим образом: $$ L(\theta) = \frac{1}{B}\sum^B_{i=1} \Bigr[ r'_i + \gamma\, Q\bigr(s'_i, \arg\max_{a'}Q(s'_i,a';\,\theta);\, \bar{\theta}\bigr) - Q(s_i,a_i;\, \theta) \Bigr]^2. $$ Сначала основная нейронная сеть $\theta$ решает, какое из следующих действий является лучшим, а затем целевая (старая) нейронная сеть оценивает это действие, чтобы узнать его Q-значение. Для реализации этого метода достаточно в методе learn_model поменять вычисление maxQ:
y = self.model(S1)
a = torch.argmax(y,1).view(-1,1) # a = arg max Q(s1,a; theta)
with torch.no_grad():
q = self.target(S1)
self.maxQ = q.gather(1, a) # Q(s1, a; theta')
Dueling DQN
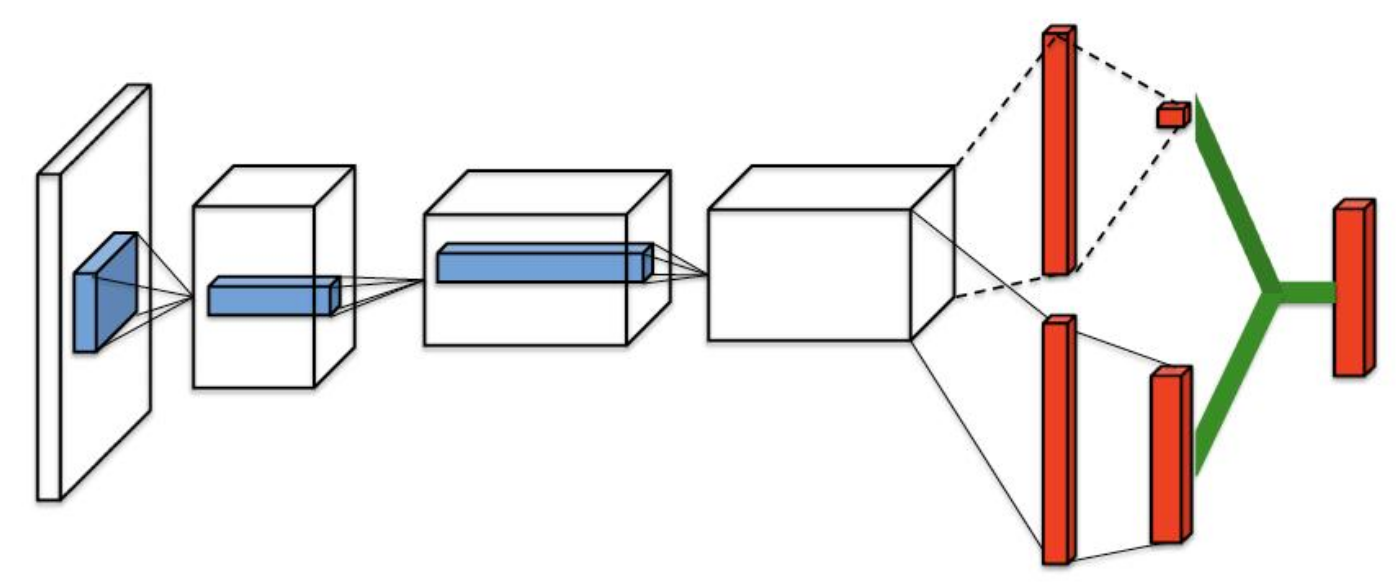В методе Dueling DQN "дуэльная" сеть расщепляется на две части.
Одна вычисляет ценность состояния $V(s)$, а вторая преимущество каждого действия
(рисунок из оригинальной статье,
в которой решалась задача видео обработки в играх Atary - свёрточные сети в начале сети).
Формально ценность состояний и действий разбивается на две части:
$$
Q(s,\,a)~=~V(s)~+~A(s,\,a),
$$
так, что
$$
V(s) = \langle Q(s,\,\pi(s))\rangle,~~~~~\langle A(s,\,\pi(s))\rangle = 0.
$$
Для детерминированной оптимальной политики:
$$
a^* = \arg\max_{a'} Q(s,a'),~~~~~~Q(s,a^*) = V(s),~~~~~~A(s,a^*) = 0.
$$
При реализации функций при помощи нейронных сетей, они зависят от параметров $\theta,\,\alpha,\,\beta$,
где $\theta$ - это общие параметры (на рисунке свёрточных сетей), а $\alpha$ и $\beta$ - параметры каждого из
полносвязных расщеплённых слоёв:
$$
Q(s,\,a;~ \theta,\,\alpha,\,\beta)~=~V(s;~\theta,\,\beta)~+~A(s,\,a;~\theta,\,\alpha).
$$
Первое слагаемое соответствует верхнему пути на рисунке, а второе - нижнему.
Выходной слой - это значения Q для каждого действия.
Вообще говоря, функции $V$ и $A$ неоднозначны и можно в $V$ прибавить константу, а из $A$ её вычесть.
Для устранения этой неоднозначности (и повышения стабильности метода) из $A$ вычитается её максимальное значение по всем действиям (параметры опускаем):
$$
Q(s,\,a)~=~V(s)~+~ \left[A(s,\,a)~-~\max_{a'}~ A\left(s,\,a'\right)\right]
$$
Теперь:
$$
a^* = \arg\max_{a'} Q(s,a') = \arg\max_{a'} A(s,a')~~~~~~~~~\Rightarrow~~~~~~~~Q(s,a^*)=V(s).
$$
Впрочем, авторы выяснили, что лучше работает вычитание среднего по всем $N_a$ действиям:
$$
Q(s,\,a)~=~V(s)~+~ \left[A(s,\,a)~-~\frac{1}{N_a}~\sum_{a'} A\left(s,\,a'\right)\right]
$$
Дополнительная информация
