|
QuData Statistical Calculator
allows to calculate different statistical parameters of the sample of random numbers.
At first, enter the sample of random values. Copy the column of random
numbers from data file or electronic table and paste them into the left vertical data
field. Then click the button "Calc". You can generate a set of normally distributed
random numbers. The button "Sort" allows you to sort the sample by values. You can
use this function to exclude several outliers values and then to repeat the calculation.
The figure in QuData Statistical Calculator shows the histogram of the sample and probability density of normal distribution. The mean and variance of normal distribution are equal to sample mean and standard deviation. Statistical Calculator allows to calculate a lot of statistical parameters of the sample (num, mean, sigma, etc. ), that are defined in Glossary. Maximum volume of the sample allowed is 100 000 values.
Definitions of statistical parameters that can be calculated with QuData Statistical Calculator:
 Glossary
Glossary
- num - number of values in the sample (the volume of sample)
- min, max - the minimal and maximal values in the sample. Range of the sample is defined as range = max - min
- mean - sampling mean calculated as:
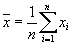
The mean value of population containing given sample can be estimated using the sample parameters: sampling mean and standard deviation. If the population of random numbers is characterized by normal distribution and the volume of sample is large enough (num > 30) then population mean lies inside confidence interval with the probability P(t):
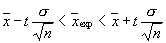
The frequently used values of confidence probability P(t) are:
| t |
1.00 |
1.96 |
2.00 |
2.58 |
3.00 |
| P(t) |
0.6827 |
0.9500 |
0.9545 |
0.9901 |
0.9973 |
The well-known rule of three sigma notes that, with probability 0.9973, the population mean can not deviate from mean, calculated by QuData Statistical Calculator, more than on 3 * sigma divided by square root of number.
For small samples with number < 30 one has to apply Student's criterion for calculating the confidence interval.
- The square of sigma is variance - the mean square of deviations of values from the sampling mean.
- sigma - (Standard Deviation) is a square root of variance:
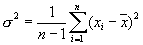
- deviation - is the mean of absolute deviations of sample values from mean
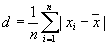
- median - the number that divides the sample points into two equal groups (random values from the sample can be more or less than this parameter with equal probability).
- lquart - Lower Quartile. The value below which 25% of the data sample fall.
- uquart - Upper Quartile. The value above which 25% of the data sample lie.
Also the Interquartile Range is sometime used, that equals to Upper Quartile - Lower Quartile.
- mode - the maximum of empirical function of distribution. QuData Statistical Calculator uses histogram to estimate the mode. Thus, its value is not precise.
- skewness - this parameter characterizes the asymmetry of distribution. If skewness > 0 then the distribution is overbalanced to the right, if skewness < 0 then the distribution is overbalanced to the left. Finally, if skewness = 0 then the distribution is symmetrical. skewness is calculated as unbiased parameter.
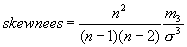
Here m3, m2 - the 3-rd and 2-nd order statistical moments. The skewness = 0 for normal distribution.
- excess - (Kurtosis) - this parameter shows the deviation of distribution from the normal one. It is calculated as unbiased parameter:
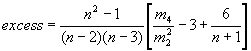
Here m4 is the statistical moment of the fourth order. The excess = 0 for normal distribution.
- moment - the statistical moment of the n-th order.
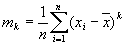
In contrast to skewness and excess the moments are biased parameters.
|
