ML: Буквенный и семантический эмбединг

Введение

В машинном обучении языковая модель предсказывает вероятности слов в тексте. Предсказываемое слово может быть очередным: $P(w_{t+1}| ...,w_{t-1},w_t)$ или замаскированным: $P(w_{t}| ...w_{t-1},?,w_{t+1},...)$. Классический подход построения языковых моделей состоит в использовании n-грамм с их последующим сглаживанием (марковские модели). Слабым местом такого подхода являются редкие n-граммы, с которыми достаточно успешно борются нейронные сети при помощи механизма эмбединга. Так, если некоторое сочетание слов в корпусе не встретилось, но их векторы со-направлены к более частотным словам, то можно получить вполне релевантную вероятность n-граммы.

У стандартного эмбединга, в свою очередь, есть два унаследованных от n-грамм недостатка:

Например, слова "молоток" и "молотком" при составлении словаря считаются не связанными друг с другом. Это снова создаёт проблемы для редких слов, которые при обучении должны встретиться в схожем контексте во всех своих словоформах (чтобы получились близкие векторы эмбединга).

С морфологической изменчивостью можно бороться при помощи классического морфологического анализа, используя лемматизацию (приведение слова к базовой форме при помощи словаря) или стемминг (выделение основы слова, путём обрезания его окончания по простым правилам). Первый метод требует больших морфологических словарей и не всегда однозначен ("стекло" = стекло - сущ. или стекать - гл.). Второй метод может справляться с незнакомыми словами, но иногда ошибается в достаточно частотных словах (например PorterStemmer для "healthy" даёт "healthi"). Ещё один подход - это добавление к вектору словоформы, векторов эмбединга его n-грамм букв (fastText). Наконец, можно сразу с уровня слов "опуститься" на уровень символов (2015). Именно этот подход подробнее рассматривается ниже.

Семантическая неоднозначность приводит к тому, что слово может иметь совершенно различные значения, однако с ним связывается один и тот-же вектор эмбединга (например "table" - стол, таблица). Один из способов уменьшения этой проблемы делается в контекстно зависимой векторизации ELMo, которая также рассматривается в этом документе.

Морфологический анализ

Рассмотрим сначала инструменты, использующиеся в классическом морфологическом анализе. Стандартом стемминга в английском языке является Стеммер Портера. Его реализация есть в библиотеке nltk: 
import nltk

ps = nltk.stem.PorterStemmer()

for w in ["looked", "decided",  "got",  "are", "parents", "feet",  "unhealthy"]:
    print(ps.stem(w), end=", ")
         # look, decid, got, are, parent, feet, unhealthi

В этой же библиотеке есть лематизатор на основе словаря WordNet. Для корректной работы, ему необходимо передавать предполагаемую часть речи (по умолчанию - это существитльное 'n'): 

nltk.download('wordnet')
wn = nltk.WordNetLemmatizer()

for p in ['n', 'v']:
    for w in ["looked", "decided",  "got",  "are", "parents", "feet",  "unhealthy"]:
        print(wn.lemmatize(w, pos=p), end=", ")        
    print()
             # looked, decided, got, are, parent, foot, unhealthy 
             # look,   decide,  get, be,  parent, feet, unhealthy

Другие библиотеки, осуществляющие лемматизацию, приведены в этом обзоре.

Буквенный эмбединг

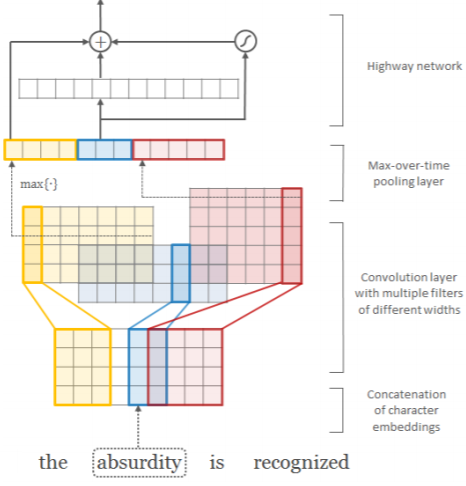В статье Kim Y., et al. (2015) было предложено получать эмбединг слов из эмбединга их букв. Для этого используются свёрточные слои (CNN) и слой макс-пулинга (подробности на рисунке справа и далее в тексте).

Пусть число символов в языке равно C и каждому из них ставится в соответствие E-мерный вектор эмбединга. Тогда слово из L букв $c_1,...,c_L$ характеризуется матрицей $\mathbf{C}$ формы (E,L) (векторы слов расположены по колонкам). К этой матрице применяется CNN-фильтр $\mathbf{H}$: (E,W), шириной W, после которого добавляется смещение $b$ и результат пропускается через функцию активации: $$ \mathbf{f}[i]= \tanh\bigr( \{\mathbf{C}[:,\,i:i+W]\odot\mathbf{H}\}.\text{sum}() + b \bigr), $$ где $\odot$ - операция поэлементного умножения матриц (без свёртки). В результате получается (L-W+1)-мерный вектор признаков $\mathbf{f}$. К этому вектору применяется max-pooling, т.е. выбирается его максимальная компонента. Эти числа по всем фильтрам объединяются в вектор эмбединга слова. Его размерность равна числу фильтров и не зависит от их ширин (каждый фильтр порождает один признак). Предполагается, что разные ширины фильтров соответствуют различным n-граммам букв.

Справа на рисунке к слову "absurdity" (L=9, E=4) применяется 12 фильтров: 4 желтых (W=3), 3 синих (W=2) и 5 красных (W=4). Векторы результатов свёртки расположены построчно.

Для использования пакетного обучения, авторы сделали одинаковыми длины всех слов, забивая нулями отсутствие букв (zero-padding). Кроме этого, каждое слово было окружено специальными стартовым и финальным символами (чтобы облегчить фильтру выделять префикс и суффикс слова). В большой модели (LSTM-Char-Large) использовался следующий набор ширин фильтров: W = [1, 2, 3, 4, 5, 6, 7] с числом фильтров для каждой ширины F = [50, 100, 150, 200, 200, 200, 200] (всего 1100 фильтров = размерность эмбединга слова). Маленькая модель (LSTM-Char-Small) содержала 525 фильтров.

Получившийся вектор $\mathbf{x}$ слова далее пропускают через полносвязную скоростную сеть (см. ниже). Векторы эмбединга на её выходе использовались авторами для построения языковой модели. Для этого, при помощи стопки однонаправленных LSTM рекуррентных слоёв, предсказывалось очередное слово последовательности. Если на входе модели могли быть любые слова (буквенный эмбединг), то на выходе рекуррентного слова стоял полносвязный слой с числом нейронов равных числу слов некоторого фиксированного словаря. Далее, как обычно, функция softmax выдавала вероятности слов.

Анализ по ближайшим соседям слов показывает, что вектор эмбединга после свёрточной сети в основном характеризует буквенное представление слова, т.е. морфологию (что и не удивительно). После скоростной сети вектор уже меньше привязан к форме и содержит семантические (контекстно независимые) признаки слов.

☝ Полносвязная скоростная сеть (highway network, 2015) состоит из стопки слоёв следующего вида: $$ \mathbf{x}' = \mathbf{t}\odot g(\mathbf{x}\cdot\mathbf{W}+\mathbf{b}) + (\mathbf{1}-\mathbf{t})\odot \mathbf{x}, ~~~~~~~~~~~~~~~ \mathbf{t}=\sigma(\mathbf{x}\cdot\mathbf{W}_T+\mathbf{b}_T). $$ Матрицы $\mathbf{W},\,\mathbf{W}_T$ квадратные и соответственно размерность выхода сети $\mathbf{x}'$ совпадает с размерностью её входа $\mathbf{x}$. В этой сети, выход обычного полносвязного слоя с активационной функцией $g$ (например ReLU) смешивается с его входом. Веса $\mathbf{t}$ смешивания определяются гейтом перобразования (transform gate), а $\mathbf{1}-\mathbf{t}$ являются гейтом переноса (carry gate). По аналогии с LSTM, эта сеть позволяет перенести некоторые признаки (компоненты $\mathbf{x}$) без изменения от входа к выходу.

Типы языковых моделей и RNN

Пусть есть последовательность из $N$ токенов (слов или букв): $w_1,...,w_N$. Прямая языковая модель (forward language model) оценивает вероятности по истории слева-направо (марковское цепное правило): $$ p(w_1,...,w_N) = \prod^N_{k=1} p(w_k|w_1...w_{k-1}). $$

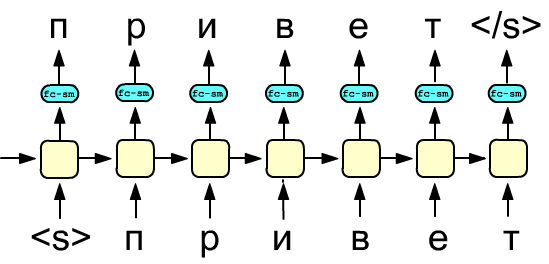
Условные вероятности $p(w_k|w_1,...,w_{k-1})$ можно получать при помощи стопки $L$ рекуррентных слоёв с номерами $j=[1...L]$. Пусть $h_{kj}$ - скрытое состояние $k$-той ячейки на $j$-м слое. Тогда, при подаче на вход первого слоя контекстно независимых векторов слов (не знающих контекста), на ячейке $h_{kL}$ последнего слоя получаются (после полносвязного слоя и softmax-функции) распределение вероятностей для слова $w_{k+1}$.

Справа приведен простейший вариант такой сети с одним рекуррентным слоем. Жёлтые блоки являются LSTM или GRU ячейками, скрытое состояние которых передаётся как на выход, так и в следующую ячейку. Голубой блок - это полносвязный слой (fc), после которого стоит софтмакс функция (sm), выдающая "вероятности" токенов. Значение входа (внизу) и выхода (вверху) приведены в процессе принудительного обучения (teacher forcing) обучения сети. Ошибку при обратном распространении можно вычислять как по всем выходам, так и по нескольким последним (после накопления информации о последовательности).

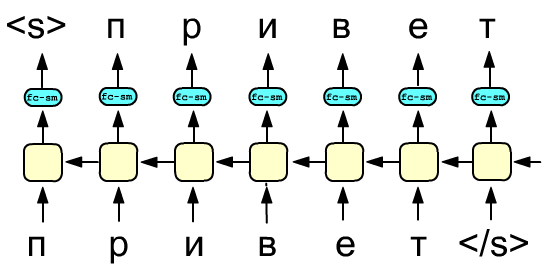Аналогично можно использовать предсказание на основе будущего контекста (future context): $$ p(w_1,...,w_N) = \prod^N_{k=1} p(w_k|w_{k+1}...w_{N}), $$ что также моделируется при помощи рекуррентных слоёв, но с обратным потоком скрытых состояний. Заметим, что, если в сети прямого соединения предсказываемая последовательность (выход слоя) сдвинута влево, то для обратного потока она должны быть сдвинута вправо.

Наконец, двунаправленная рекуррентная сеть, основанная на двух встречных RNN-слоях, может максимизировать следующую величину: $$ \sum^N_{k=1}\Bigr[ \log\,p(w_k|w_1...w_{k-1}; \overrightarrow{\Theta\,}_f )+ \log\,p(w_k|w_{k+1}...w_{N}; \overleftarrow{\Theta}_b) \Bigr], $$ где символ $\overrightarrow{\Theta\,}_f$ означает параметры ячейки RNN, соединённые слева-направо, а $\overleftarrow{\Theta\,}_b$ - справа-налево. Просто воспользоваться двунаправленной сетью для построения такой языковой модели нельзя и требуются некоторые изменения.

Обучение на неразмеченных данных

Ниже на первом рисунке приведены значения входов и выходов двунаправленной рекуррентной сети в процессе её принудительного обучения. Нижний слой предсказывает следующий токен, а верхний - предыдущий. Для генерации текста (в процессе тестирования) такая архитектура не подходит. Однако, иногда необходимо иметь интегральную информацию о тексте, например, для задачи определения тональности предложения (sentiment analysis) или для получения морфологического вектора слова по векторам эмбединга его букв. В этом случае, двунаправленная модель обучается на неразмеченных данных предсказывать сдвинутую последовательность так, как представлено на рисунке. В режиме использования обученной сети на её входы подаётся последовательность токенов и скрытые состояния слоёв (все или последние) объединяются (конкатенируются). Полученный вектор далее используется для решения конкретных задач. Например, для определения тональности текста он пропускается через полносвязный слой, веса которого обучаются уже на размеченных данных.

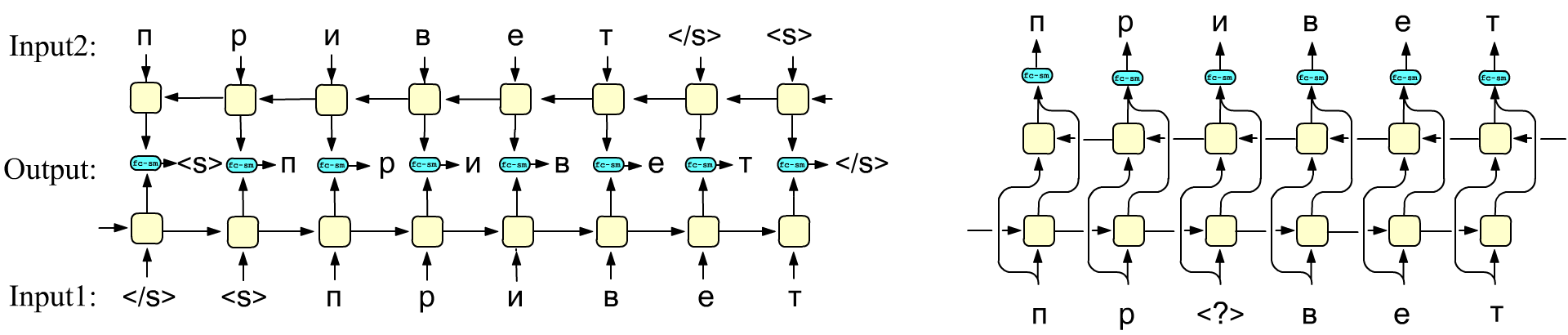
Справа приведена другая стратегия обучения, которая была применена в архитектуре BERT (но вместо рекуррентных слоёв там использовался энкодер трансформера). В этом подходе обычная двунаправленная сеть (возможно состоящая из нескольких слоёв) в режиме обучения должна выдавать на выходе входную последовательность без смещения. При этом, часть токенов входной последовательности "прячутся", заменяясь на выделенный токен (на рисунке это <?>). Такое обучение на неразмеченных данных формирует языковую модель, которую далее можно использовать в различных задачах.

Наконец, можно обучать независимым образом две сети (с направлением слева-направо и справо-налево). Затем конкатенировать их выходы. Полученную конкатенацию выходов встречных слоёв каждой пары ячеек (вектор перед fc-sm блоком) можно использовать в качестве контекстно-зависимого эмбединга токенов. Действительно, в этих скрытых состояниях содержится информация не только о текущем входном токене, но и обо всей последовательности.

Смесь эмбедингов

Для формирования морфологического вектора эмбединга слова, по-мимо свёрточных сетей, можно также использовать рекуррентные сети. Для этого берётся двунаправленная сеть (обычно из одного слоя). На её вход поступают векторы эмбедингов букв. "Морфологическая модель" в процессе обучения тренируется определять на выходе, например, замаскированную букву (выше второй рисунок). Далее берётся конкатенация последних скрытых состояний каждого слоя (запомнивших слово "от начала к концу" и "от конца к началу").

Так как подобный способ эмбединга концентрируется только на морфологии, его объединяют с обычным "семантическим" эмбедингом. Для этого в простейшем случае производится конкатенация морфологического и семантического векторов эмбедига. При совпадении размерностей их можно также складывать. Последний случай хорош для редких слов. Даже если их семантический эмбединг получен не очень хорошо (например, слово в редко встречается в каком-то склонении), его сумма с морфологическим вектором, делает его похожим на вектор, например, основной формы этого слова.

Естественно, после предварительного и независимого обучения морфологическому и семантическому эмбедингу, можно проводить их совместную тонкую настройку.

Обычно модель на выходе даёт номер слова из фиксированного словаря. В принципе, вместо этого, она может порождать буквенную запись слова. Для этого вектор слова (после прохождения модели) подаётся, например, на рекуррентную однонаправленную сеть, которую учат выдавать последовательность букв, соответствующую данному вектору.

ELMo

ELMo (Embeddings from Language Models) - является методом эмбединга, который учитывает контекст предложения, снимая тем самым семантическую неоднозначность, присущую обычному эмбедингу. В этом методе языковую модель создают в результате обучения стопки двунаправленных рекуррентных слоёв. Затем обученная сеть используется как "поставщик" контекстно зависимых векторов эмбединга слов. Эти векторы являются суммой скрытых состояний всех слоёв с некоторыми коэффициентами, которые служат параметрами обучения уже в конкретной задаче. Рассмотрим эту идею детальнее.

Пусть есть стопка из $L$ двунаправленных рекуррентных слоёв. Обозначим обычный (контекстно независимый) вектор эмбединга $k$-того слова, поступающий на вход $k$-той ячейки первого слоя как $\mathbf{h}_{k0}$. Конкатенацию скрытых состояний $k$-той ячейки $j$-того двунаправленного слоя обозначим как $\mathbf{h}_{kj}=[\mathbf{h}^\rightarrow_{kj},\, \mathbf{h}^\leftarrow_{kj}]$, где $\mathbf{h}^\rightarrow_{kj}$ - скрытые состояния слоя с прямым проходом, а $\mathbf{h}^\leftarrow_{kj}$ - с обратным. В качестве контекстно зависимых векторов эмбединга берётся линейная комбинация скрытых состояний всех слоёв:

$$ \mathbf{v}_k = \gamma \sum^L_{j=0} s_j\,\mathbf{h}_{kj},~~~~~~~~~~~~~~~~~~~\sum^N_{j=0} s_j = 1. $$ Сумма коэффициентов $s_j$ равна единице (что обеспечивается функцией softmax), а $\gamma$ является общим масштабирующим множителем.

Сеть обучается на неразмеченном корпусе текстов предсказывать слова. Затем веса слоёв "замораживают" и сеть используется как поставщик компонент $\mathbf{h}_{kj}$ контекстно зависимых векторов в формуле выше. При этом параметры $s_j$ и $\gamma$ подбирают в рамках размеченных обучающих данных в рамках конкретной задачи.

Литература

Статьи