ML: Neural Networks in Torch – Reference Guide

Interfaces for layers

Layers in PyTorch are implemented in two forms: as functions and as classes.

The first form consists of regular functions that take layer parameters and an input tensor. For example, a linear layer multiplies an input matrix of shape (N, nX) by the transposed weight matrix W of shape (nY, nX) and optionally adds a bias vector. The output is a tensor of shape (N, nY):

import  torch.nn.functional as F

N, nX, nY = 1, 2, 3                               # number of samples, inputs, outputs
X = torch.ones(N,  nX)                            # matrix of samples
W = torch.ones(nY, nX)                            # weight matrix 
B = torch.ones(nY)                                # bias vector

Y = F.linear(X, W, B)                             # [[3., 3., 3.]]
Y = X.mm(W.t())+B                                 # same thing
Y = torch.addmm(B,X,W.t())                        # same thing

import torch.nn as nn

fc =  nn.Linear(nX, nY)
Y  = fc(X)                                        # tensor([[-0.1559, -0.2140, 0.1462]],
                                                  #         grad_fn=<Addmm>)

The layer class sets requires_grad=True for its parameters. This results in a computational graph being built during forward propagation and gradients being obtained for the parameters during backpropagation:

print(fc.bias)            # tensor([ 0.529, -0.103,  0.646], requires_grad=True)
print(fc.bias.is_leaf)    # True
print(fc.bias.grad)       # None

L = torch.sum(Y*Y)        # scalar "loss function"
L.backward()              # start gradient computation
fc.bias.grad              # tensor([-0.3688,  0.6441, -1.6415])

What follows is a brief reference of the most important types of layers, activation functions, and optimizers. For more detailed information, refer to the documentation.

Basic layers

Fully connected layer

Performs a linear transformation $\mathbf{y} = \mathbf{x}\cdot \mathbf{W}^T + \mathbf{b}$. The layer parameters are stored in the weight and bias attributes. The weight matrix $\mathbf{W}$ is stored in transposed form (so that when multiplying matrices $\mathbf{X}\mathbf{W}^\top$ their rows are used, not a row and a column). If you need to set the weights manually, this is done outside the computation graph:

fc = nn.Linear(nX, nY)
with torch.no_grad():
    fc.weight.copy_(W)     # set the weight matrix
    fc.bias.  copy_(B)     # set the bias vector

The implementation of a linear layer in torch.nn.functional looks as follows:

def linear(X, weight, bias=None):
    if X.dim() == 2 and bias is not None:       # fused op is marginally faster 
        ret = torch.addmm(bias, X, weight.t())  # bias + X @ weight.t()
    else:
        output = X.matmul(weight.t())
        if bias is not None: output += bias
        ret = output
    return ret

Let in_features=nX, out_features=nY and assume there is a bias term: bias=True. The input tensor may have an arbitrary number of indices (ellipsis), and the layer transforms its shape as follows: (N,...,nX) -> (N,...,nY).
The number of parameters in the layer is nX*nY + nY.

Embedding

The Embedding layer transforms an array of integers of type long at the input into a matrix (an array of vectors). For more details, see Word Embedding. When creating a layer instance, the first two parameters are mandatory: vocabulary size and embedding dimension. Below, a layer is created with 5 words and their 2-dimensional (random) vectors:

emb = nn.Embedding(5, 2)

X = torch.tensor([0,2,1])

print (emb(X))
print(emb.weight)

tensor([[-1.3062, -1.6261],
        [-0.3903,  0.0998],
        [ 0.2643,  1.6466]],  grad_fn=<Embedding>)
Parameter containing:
tensor([[-1.3062, -1.6261],
        [ 0.2643,  1.6466],
        [-0.3903,  0.0998],
        [-0.5463, -0.5028],
        [ 1.3299, -0.0580]],  requires_grad=True)

The parameter max_norm sets the maximum vector length, and if during training it is exceeded, the vector is renormalized. The default norm is the sum of squares of components: norm_type = 2.

With scale_grad_by_freq = True, gradients during training are scaled by the inverse frequency of words in the batch (strengthening changes for rarer words). But the batch should be sufficiently large in this case. You can load pretrained vectors by creating a layer as follows:

weight = torch.FloatTensor([[1, 2.3, 3], 
                            [4, 5.1, 6]])
emb = nn.Embedding.from_pretrained(weight)    # Create a layer with pretrained vectors
input = torch.LongTensor([1])                 # Get embeddings for index 1
emb(input)                                    # tensor([[ 4.0,  5.1,  6.0]])

from_pretrained(embeddings, freeze=True, padding_idx=None, 
                max_norm=None, norm_type=2.0, scale_grad_by_freq=False, sparse=False)

Convolution

The Conv2D convolutional layer is applied to “images” with height rows, width cols, and in_channels color channels. In reality, these graphical terms are conventional, and the Conv2D layer can be used not only for image processing. The shape of the input tensor is (N, in_channels, rows, cols). The output will be a tensor of shape (N, out_channels, rows_out, cols_out). The original tensor is scanned by out_channels filters of size kernel_size (a number or a tuple). The depth of each filter is determined by the number of input channels in_channels.

In the illustration below, in_channels=2, out_channels=3 (three filters), and the filter size is kernel_size = 2, or equivalently kernel_size = (2,2). By default, filters slide over the image with stride one stride=(1,1), so the resulting image width and height decrease by 1:

The padding parameter (int or tuple) specifies how many “pixels” to add to each side of the image before filtering. The extended region is filled according to the padding_mode parameter: 'zeros', 'reflect', 'replicate', 'circular'. The parameter dilation = 1 sets the spacing between pixels included in the filter.

As an example, let’s create a 3x4 “image”, whose left half is white (1) and right half is black (0), and apply to it a 2x2 filter that highlights a vertical edge:

X = torch.zeros(1,1,3,4)
X[0,0,:,:2] = 1
print(X)

conv = nn.Conv2d(1,1,kernel_size=2,bias=False)
print( conv ) 

with torch.no_grad():
    conv.weight.copy_(torch.tensor([[-1.,1.], 
                                    [-1.,1.]]))

print( conv.weight )
print( conv.bias )
print( conv(X) )

tensor([[[[1., 1., 0., 0.],
          [1., 1., 0., 0.],
          [1., 1., 0., 0.]]]])
          
Conv2d(1,1,kernel_size=(2,2),stride=(1,1))


# set the filter core
tensor([[[[-1.,1.],
          [-1.,1.]]]],requires_grad=True)
None
tensor([[[[ 0., -2.,  0.],
          [ 0., -2.,  0.]]]], 
          grad_fn=<ThnnConv2D>)

RNN

The basic recurrent layer computes a new hidden state $\mathbf{h}^{(t)}$ from the input $\mathbf{x}^{(t)}$ and the previous hidden state $\mathbf{h}^{(t-1)}$: $$ \mathbf{h}^{(t)} = \tanh(\mathbf{x}^{(t)}\,\mathbf{W}_{ih} + \mathbf{b}_{ih} + \mathbf{h}^{(t-1)}\,\mathbf{W}_{hh} + \mathbf{b}_{hh}) $$

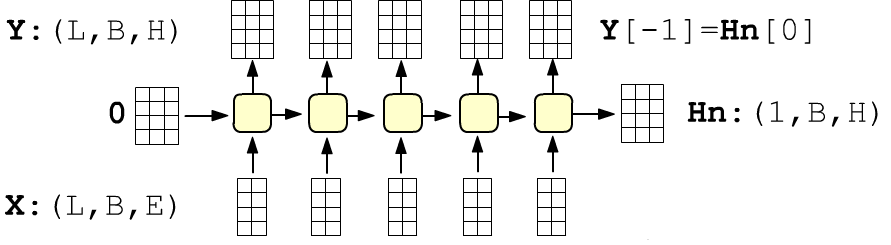
Required parameters: input_size - the dimensionality of the inputs ($\mathbf{x}$) and hidden_size - the dimensionality of the output (= the hidden state $\mathbf{h}$).

By default, the input has shape (seq_len, batch_size, input_size), where seq_len is the number of RNN cells (inputs). The batch index can be made the first dimension using the batch_first parameter. However, this default tensor shape usually appears automatically if an Embedding layer with seq_len inputs and vector dimensionality input_size = VEC_DIM precedes the RNN layer.

The layer returns a tuple consisting of a tensor of all network outputs with shape (seq_len, batch_size, hidden_size) and the last hidden state (the final output) with shape (num_layers, batch_size, hidden_size), where for a single layer num_layers = 1. By default, the components of the initial hidden state are zeros. Otherwise it can be passed as the second argument:

X_dim  = 2           # input dimensionality          = dim(x)
H_dim  = 4           # hidden state dimensionality   = dim(h)
L      = 3           # number of inputs (RNN cells)
B      = 1           # number of examples (batch_size)

rnn = nn.RNN(X_dim, H_dim)

X  = torch.zeros(L, B, X_dim)
H0 = torch.zeros(1, B, H_dim)     

Y, Hn = rnn(X, H0)                       # H0 is optional, default is zero

print(tuple(Y.shape), tuple(Hn.shape))   #  (3, 1, 4) (1, 1, 4)
print(Y[-1] == Hn[-1])                   #  tensor([[[True, True, True, True]]])

You can create a stack of RNN layers at once using num_layers. Between layers, you can insert a mode of randomly filling outputs with zeros with a probability of dropout. The layer can also be made bidirectional: bidirectional = True. In this case, the output shape becomes (inputs, batch_size, 2*hidden_size), and the initial hidden state has shape (2 * num_layers, batch_size, hidden_size).

LSTM

Similar to RNN. For details, see NN_RNN.html. In addition to the hidden state $\mathbf{h}$, it has a cell memory $\mathbf{c}$, see the documentation.

rnn = nn.LSTM(10, 20, 2)
...
output, (hn, cn) = rnn(input, (h0, c0))

MultiheadAttention

Inputs: Q:(L,N,E), K,V:(S,N,E), where L - is the target sequence length (for the decoder),
N - is the batch size, E - is the embedding dimension (embed_dim), S - is the source sequence length.

Outputs: output: (L,N,E), weights: (N,L,S)

Matrix dimensions: $\mathbf{W}^Q:$ (E, E), $\mathbf{W}^K:$ (E, kdim), $\mathbf{W}^V:$ (E, vdim), where kdim, vdim are specified or equal to E, but they are passed to the linear function, therefore they are transposed during multiplication.
The dimension of each head is head_dim = E // num_heads.
The output matrix $\mathbf{W}^O:$ is the layer Linear(E, E, bias=bias).
If bias is present, it is added after multiplying by the projection matrices $\mathbf{W}^Q,\mathbf{W}^K,\mathbf{W}^V$ (each has its own).

If the embedding of the inputs is the same, then the projection matrices are packed into in_proj_weight with shape (3*E, E), otherwise these are the parameters: q_proj_weight, k_proj_weight, v_proj_weight. The bias (if present) is in_proj_bias with shape (3*E,), and the output layer is out_proj.

Conceptually, the following computations take place (N is the batch size, see details in NN_Attention.html):

q = linear(Q, q_proj_weight, in_proj_bias[0 : E])     # (L,N,E) @ (E, E).T    = (L,N,E)
k = linear(K, k_proj_weight, in_proj_bias[E : E*2])   # (S,N,E) @ (E, kdim).T = (S,N,kdim)
v = linear(V, v_proj_weight, in_proj_bias[E*2:])      # (S,N,E) @ (E, vdim).T = (S,N,vdim)

q = q.contiguous().view( L, N * num_heads, head_dim).transpose(0,1)
k = k.contiguous().view(-1, N * num_heads, head_dim).transpose(0,1)
v = v.contiguous().view(-1, N * num_heads, head_dim).transpose(0,1)

a_weights = torch.bmm(q, k.transpose(1,2))
a_weights = softmax(a_weights, dim=-1)

a = torch.bmm(a_weights, v)

a = a.transpose(0, 1).contiguous().view(L, N, E)
a = linear(a, out_proj_weight, out_proj_bias)

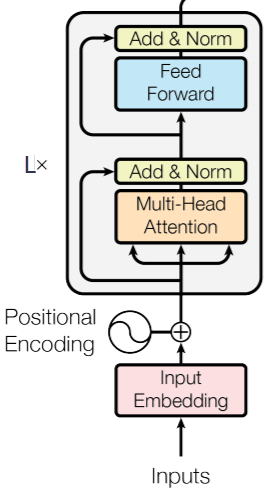
TransformerEncoderLayer

Parameters: d_model – the input dimension (a single token vector), nhead – the number of heads (a divisor of d_model), dim_feedforward – the dimension of the feedforward network.

TransformerEncoder

L, N, E = 10, 32, 512            # number of tokens, batch size, embedding dimension

encoder_layer       = nn.TransformerEncoderLayer(d_model=E, nhead=8)
transformer_encoder = nn.TransformerEncoder     (encoder_layer, num_layers=6)

src = torch.rand(L, N, E)
out = transformer_encoder(src)   # out.shape == src.shape

Layers without parameters

Tensor flattening

With default parameters, all dimensions except the first one (the sample index) are merged into a single dimension (each sample becomes a vector). This layer has no parameters.

X = torch.ones(2, 5,4,3)
Y = torch.nn.Flatten()(X)
print( tuple(Y.shape) )                   # (2, 60)

Cosine between vectors

$$ \frac{\mathbf{u}\mathbf{v}}{ \max( |\mathbf{u}|\,|\mathbf{v}|,~~\epsilon) } $$

u, v = torch.randn(100, 128), torch.randn(100, 128)
output = nn.CosineSimilarity(dim=1, eps=1e-6) (u, v)

Distance between vectors

$$ \bigr(\sum_{i} |x_i|^p \Bigr)^{1/p} $$

Disabling neurons

In training mode: m.train(), each element of the matrix is zeroed out with probability "p" and the remaining elements are divided by 1-p.
In evaluation mode: m.eval(), nothing happens. Because of the division by 1-p, the average absolute value of elements during training remains the same as in evaluation mode (i.e., equal to the input tensor).

m = nn.Dropout(p = 0.2)
                               #                     v                      v
print( m(torch.ones(10)) )     # [1.25, 1.25, 1.25, 0.0, 1.25, 1.25, 1.25, 0.0, 1.25, 1.25]

x = torch.randn(100, 100)

m.eval()                       # This is equivalent with self.train(False)
y = m(x)
print( (x==y).float().mean() ) # unchanged

m.train() 
y =m(x)

print(x.abs().mean(),   (x*x < 1e-10).float().mean()  )   # 0.8025     0.
print(y.abs().mean(),   (y*y < 1e-10).float().mean()  )   # 0.8001     0.206

Tensor normalization

Across the batch (the first index), mean values and variances are computed independently for each feature. Then the data is normalized and shifted affinely using trainable parameters $\gamma,\,\beta$: $$ y = \frac{x - \mathrm{E}[x]}{\sqrt{\mathrm{Var}[x] + \epsilon}} \odot \text{weight} + \text{bias} $$ The input must be a tensor of shape (N,F) or (N,F,L). The parameter num_features = F. For a tensor (N,F,L), averaging is done over dim=0,2, i.e., the same mean for each "position" along the last index [0...L-1].

During training, mean values are smoothed using an exponential moving average with parameter momentum (if None, simple averaging is used). These running averages are stored and later used during testing (even with a single batch).

m =  nn.BatchNorm1d(2)

x = torch.randn(100000,2)
print( x.mean(dim=0), x.var(dim=0) )    # [-0.0005,  0.0067]      [1.0058, 0.9956]

x = 2 *  x + 3 
print( x.mean(dim=0), x.var(dim=0) )    # [ 3.0010,  2.9867]      [4.0231, 3.9824]

y = m(x)
with torch.no_grad():
    print(y.mean(dim=0), y.var(dim=0))  # [ 0.0000,  0.0000]      [1.0000, 1.0000]
    
    
for k, v in m.state_dict().items():     # weight             :(2,)
    print(f'{k:20s}: {tuple(v.shape)}') # bias               :(2,)
                                        # running_mean       :(2,)
                                        # running_var        :(2,)
                                        # num_batches_tracked:(  )

MaxPool2d

AvgPool2d

Activation functions

X = torch.tensor( [ [1.,2.,3] ] )
torch.nn.Softmax(dim=1)(X)              # tensor([[0.09, 0.24, 0.66]])

Loss functions

Mean squared error

✒ nn.MSELoss
… (size_average=None, reduce=None, reduction='mean') [doc] $$ L(y,\hat{y}) = (y - \hat{y})^2 \left\{ \begin{array}{ll} .\mathrm{mean}() & \text{if reduction='mean'}\\ .\mathrm{sum}() & \text{if reduction='sum'} \end{array} \right. $$

By default (reduction='mean'), the squared deviations are averaged over all batch examples and over all outputs (the loss is a scalar!).

loss = torch.nn.MSELoss()

y  = torch.rand(10, 2)                  # 10 samples, 2 outputs
yb = torch.rand(10, 2)

loss(y, yb) == ((y-yb)**2).mean()  

Binary cross-entropy

It is assumed that this loss is applied after a sigmoid activation, i.e., model outputs y and target values yb lie in the range [0...1]. Typically, BCELoss is used for a network with one output (a task with two classes 0 and 1). If classes overlap (i.e., an example may belong to several classes at once), then the number of outputs equals the number of classes. By default (reduction='mean'), errors are averaged over all examples and outputs:

loss = torch.nn.BCELoss()

y  = torch.rand(10, 2, 3)                  # 10 samples, 2x3 outputs
yb = torch.rand(10, 2, 3)

print(    loss(y, yb) )
print(  -( yb*y.log() + (1-yb)*(1-y).log() ).mean()  )

Cross-entropy

Applied to the classification task of non-overlapping $C$ classes. The network must have $C$ outputs, i.e. the loss function receives from the model a tensor $y_{i\alpha}$ of shape $(N,C)$, where $N$ is the batch size. The targets are integers $\hat{y}_i \in [0...C-1]$ — the class indices of each sample with shape (N,). The loss for a single $i$-th example with $\hat{y}_i=c$ is:

Inputs to the loss function CE_loss(y, y_t) may have the form y=(B,C):float, y_t=(B,):long or in the n-dimensional case: y=(B,C,L1,...,Ln):float, y_t=(B,L1,...,Ln):long

B, C, L = 10, 5, 4                   # samples, classes, outputs
w = torch.rand(C)                    # class importance weights

CE_loss = nn.CrossEntropyLoss(weight=w, ignore_index=1)   

y     = torch.randn(B, C, L)
yb    = torch.empty(B, L,     dtype=torch.long).random_(C)

loss  = CE_loss(y, yb)
print(loss)                          # loss

y = -nn.Softmax(dim=1)(y).log()      # minus the log of softmax 

loss, norm = 0, 0
for b in range(B):
    for l in range(L):
        c = yb[b,l]                  # correct class
        if c != 1:                   # ignore class 1
            loss += w[c]*y[b, c, l]  # loss
            norm += w[c]             # normalization
print(loss/norm)

Negative log-likelihood

The result will be the same as with CrossEntropyLoss if the final layer is LogSoftmax.

Optimizers

torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), 
                 eps=1e-08, weight_decay=0, amsgrad=False)

torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0, 
                    initial_accumulator_value=0, eps=1e-10)

torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)

torch.optim.RMSprop(params, lr=0.01, alpha=0.99, weight_decay=0, momentum=0,
                    eps=1e-08, centered=False)

torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))

torch.optim.SGD(params, lr, momentum=0, 
                dampening=0, weight_decay=0, nesterov=False)