
Перевага деревоподібних архітектур перед згортковими мережами: дослідження продуктивності
Традиційно методи навчання рішень для глибокого навчання (DL) мають свої витоки в принципах роботи людського мозку, де нейрони представлені вузлами, які пов'язані один з одним, і сила цих зв'язків змінюється, коли нейрони активно взаємодіють. Глибокі нейронні мережі складаються з трьох або більше шарів, включаючи вхідні та вихідні шари. Однак ці два сценарії навчання суттєво відрізняються. По-перше, для ефективних архітектур DL потрібні десятки прихованих шарів прямого поширення, які на цей час розширюються до сотень, в той час як динаміка мозку складається з декількох шарів прямого поширення.
По-друге, архітектури глибокого навчання зазвичай включають багато прихованих шарів, і більшість з них – це згорткові шари. Ці згорткові шари шукають певні образи або симетрії у невеликих ділянках вхідних даних. Потім, коли ці операції повторюються в наступних прихованих шарах, вони допомагають виявити значніші характеристики, які визначають клас вхідних даних. Схожі процеси спостерігалися в нашій зоровій корі, проте апроксимовані згорткові зв'язки були підтверджені головним чином від входу сітківки ока до першого прихованого шару.
Ще один складний аспект у глибокому навчанні пов'язаний з тим, що метод зворотного розповсюдження помилки, який важливий для роботи нейронних мереж, не має біологічного аналога. Цей метод змінює ваги нейронів таким чином, що вони стають більш придатними для вирішення задачі.
У процесі навчання ми надаємо мережі вхідні дані та порівнюємо, наскільки вона помиляється в порівнянні з тим, що ми очікували б отримати. Ми використовуємо функцію помилки для виміру цієї різниці.
Потім ми починаємо оновлювати ваги нейронів, щоб зменшити цю помилку. Для цього ми розглядаємо кожен шлях між входом і виходом мережі, і визначаємо, який внесок у загальну помилку робить кожна вага на цьому шляху. Ми використовуємо цю інформацію для корекції ваги.
Згорткові та повноз'єднані шари мережі відіграють важливу роль у цьому процесі, і вони особливо ефективні завдяки паралельним обчисленням на графічних процесорах. Однак варто відзначити, що такий метод не має аналогів у біології та відрізняється від того, як мозок людини обробляє інформацію.
Отже, хоча глибоке навчання потужне та ефективне, воно є алгоритмом, розробленим виключно для машинного навчання та не імітує біологічний процес навчання.
Дослідники з Університету Бар-Ілан в Ізраїлі поцікавилися, чи можна створити новий вид ефективного штучного інтелекту, використовуючи архітектуру, схожу на штучне дерево. У цій архітектурі кожна вага має лише один шлях до вихідного блоку. Їхня гіпотеза полягає в тому, що такий підхід може призвести до більш високої точності при класифікації, ніж складніші архітектури глибокого навчання, які використовують більшу кількість шарів та фільтрів. Дослідження опубліковано у журналі Scientific Reports.
В основою цієї роботи стоїть питання про те, чи може навчання на деревоподібній архітектурі, на створення якої надихнули образи дендритних дерев, досягти таких же успішних результатів, які зазвичай досягаються при використанні більш структурованих архітектур, що включають кілька повноз'єднаних та згорткових шарів.
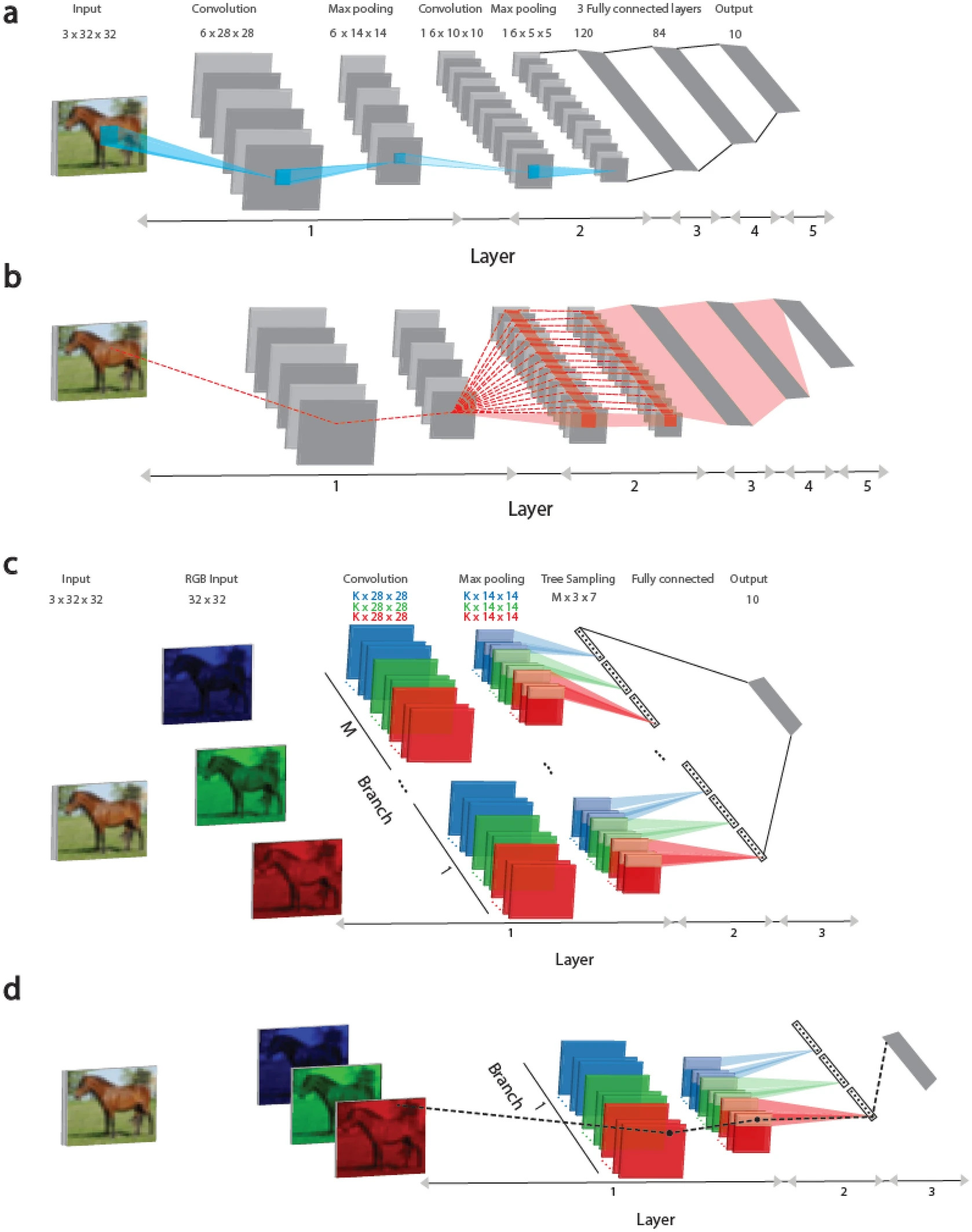
У цьому дослідженні представлено підхід до навчання, який заснований на деревоподібній архітектурі, де кожна вага підключена до вихідного блоку лише одним маршрутом, рисунок 1 (c, d). Такий підхід, це ще один крок до правдоподібної реалізації біологічного навчання, він ґрунтується на нещодавніх відомостях про те, що дендрити (частини нейрона) та їхні найближчі гілки можуть змінюватися і сигнали, що проходять через ці структури, стають сильнішими та виразнішими.
Тут показано, що показники успіху запропонованої архітектури Tree-3, яка має лише три приховані шари, перевершують досягнуті показники успіху LeNet-5 у базі даних CIFAR-10.
На рисунку 1 (а) розглянуті згорткові архітектури LeNet-5 та Tree-3. Вертикальна мережа LeNet-5 для бази даних CIFAR-10 складається з вхідних зображень RGB розміром 32 × 32, що належать 10 вихідним міткам. Перший шар складається з шести (5 × 5) згорткових фільтрів, за якими слідує (2 × 2) макс-пулінг, другий шар складається з 16 (5 × 5) згорткових фільтрів, а шари 3 - 5 мають три повнозв'язні приховані шари розміром 400, 120 та 84, які підключаються до 10 вихідних блоків.
На рисунку 1 (b) пунктирною червоною лінією визначено схему маршрутів, що впливають на оновлення показників ваги, які належать першому шару, на панелі (a) під час процедури зворотного поширення помилки. Вага підключена до одного з вихідних блоків кількома маршрутами (пунктирні червоні лінії) і може перевищувати мільйон. Важливо відзначити, що всі ваги на першому шарі прирівнюються до ваги 6 × (5 × 5), що належать шести згортковим фільтрам, рисунок 1 (c).
Архітектура Tree-3 складається з М = 16 гілок. Перший шар кожної гілки складається з K (6 або 15) фільтрів розміром (5 × 5) для кожного із трьох каналів RGB. Кожен канал згорнутий із власним набором K фільтрів, в результаті чого виходить 3 × K різних фільтрів. Фільтри згорткового шару однакові для всіх гілок M. Перший шар закінчується макс-пулінгом що складається з (2 × 2) квадратів, що не перекриваються. В результаті цього виходить (14 × 14) вихідних одиниць для кожного фільтра. Другий шар складається із вибірки дерева. Для набору даних CIFAR-10 цей шар з'єднує приховані одиниці першого шару за допомогою деревоподібної (неперетинної) вибірки (2 × 2 × 7 одиниць) за K-фільтрами для кожного кольору RGB у кожній гілці, в результаті чого для кожної гілки отримуємо 21 вихідний сигнал (7 × 3). Третій шар повністю з'єднує виходи 21 × M гілок M шару 2 з 10 вихідними модулями. Для онлайн навчання використовується функція активації ReLU, тоді як для офлайн навчання використовується Sigmoid.
На рисунку 1 (d) пунктирною чорною лінією зазначено схему одного маршруту, що з'єднує оновлену вагу на першому рівні, відображену на рисунку 1 (c) під час процедури зворотного поширення помилки з вихідним пристроєм.
Для вирішення завдання класифікації дослідники застосували функцію вартості перехресної ентропії та використали алгоритм стохастичного градієнтного спуску для її мінімізації. Для налаштування моделі найкращим чином було знайдено оптимальні гіперпараметри, такі як швидкість навчання, константа імпульсу та коефіцієнт загасання ваги. Для перевірки моделі використовувалися кілька наборів даних перевірки, що складаються з 10 000 випадкових прикладів, як і в тестовому наборі даних. Середні результати було обчислено з урахуванням стандартного відхилення від заявлених середніх показників успіху. У дослідженні було застосовано метод Нестерова та метод регуляризації L2.
Гіперпараметри для автономного навчання: η (швидкість навчання), μ (константа імпульсу) та α (регуляризація L2) – були оптимізовані для автономного навчання з 200 епохами. Гіперпараметри онлайн навчання були оптимізовані з використанням трьох різних розмірів наборів даних з прикладами.
В результаті експерименту було продемонстровано ефективний підхід до навчання деревоподібної архітектури, де кожна вага підключається до вихідного блоку лише одним маршрутом. Це наближення до біологічного навчання та спосіб використовувати глибоке навчання за допомогою сильно скорочених дендритних дерев одного або кількох нейронів. Важливо відзначити, що додавання одного згорткового шару до входу допомагає зберегти деревоподібну структуру та покращити успіх, у порівнянні з архітектурами без згортки.
Обчислювальна складність LeNet-5 виявилася значно вищою, ніж у архітектури Tree-3 з аналогічними показниками успішності. Однак для її ефективної реалізації потрібний новий тип апаратного забезпечення. Очікується також, що навчання деревоподібної архітектури зведе до мінімуму можливість виникнення вибуху градієнтів, що є однією з проблем глибокого навчання. Введення паралельних гілок замість другого згорткового шару в LeNet-5 покращило показники успіху при збереженні деревоподібної структури. Можливість того, що великомасштабні і глибші деревоподібні архітектури з розширеною кількістю гілок і фільтрів можуть конкурувати з сучасними показниками успіху CIFAR-10, заслуговує на подальше дослідження. Цей експеримент, що використовує LeNet-5 як відправну точку, наголошує на потенційних перевагах дендритного навчання та його обчислювальних можливостей.
