Чи є глибоке навчання необхідним компонентом штучного інтелекту?

У світі штучного інтелекту питання ролі глибокого навчання стає все більш центральним. Парадигми штучного інтелекту традиційно черпали натхнення з функціонування людського мозку, але виявилося, що навчання, властиве нашому мозку, має обмеження порівняно з глибоким навчанням (Deep learning). Глибоке навчання, безперечно, досягло вражаючих успіхів, проте воно має свої недоліки, включаючи високу обчислювальну складність та потребу у великому обсязі даних.

У світлі вищезазначених проблем вчені з Університету Бар-Ілан в Ізраїлі порушують важливе питання: чи необхідно включати глибоке навчання до складу штучного інтелекту? Вони представили свою нову роботу, опубліковану в журналі Scientific Reports, яка продовжує їхнє попереднє дослідження про перевагу деревоподібних архітектур перед згортковими мережами. Основною метою нового дослідження стало з'ясувати, чи можна ефективно навчати складні завдання класифікації, використовуючи менш глибокі нейронні мережі, що ґрунтуються на принципах, які базувалися на роботі мозку, і при цьому знижувати обчислювальне навантаження. У цій статті ми викладемо ключові результати дослідження, які можуть переписати правила гри для сфери штучного інтелекту.

Отже, як ми вже знаємо, для успішного вирішення складних завдань класифікації потрібне навчання глибоких нейронних мереж, що складаються з десятків або навіть сотень згорткових і повнозв'язкових прихованих шарів. Це суттєво відрізняється від того, як функціонує людський мозок. В рамках глибокого навчання перший згортковий шар виявляє локалізовані патерни у вхідних даних, а наступні шари визначають більш масштабні патерни, поки не буде досягнуто надійної характеристики класу вхідних даних.

У цьому дослідженні показано, що при використанні фіксованого співвідношення глибини першого і другого згорткових шарів помилки в невеликій архітектурі LeNet, що складається всього з п'яти шарів, зменшуються зі збільшенням кількості фільтрів в першому згортковому шарі по степеневому закону. Екстраполяція цього степеневого закону дозволяє стверджувати, що узагальнена архітектура LeNet здатна досягати низьких значень помилок аналогічно тим, що є результатом використання глибоких нейронних мереж на базі даних CIFAR-10.

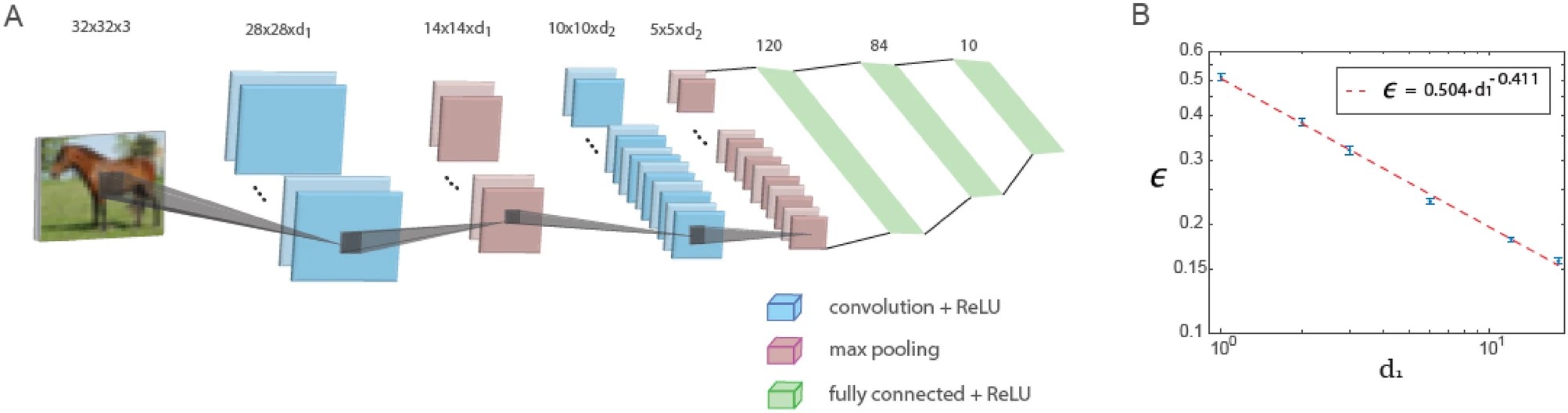
На рисунку нижче показано навчання в узагальненій архітектурі LeNet. Узагальнена архітектура LeNet для бази даних CIFAR-10 (розмір вхідних даних 32 x 32 x 3 пікселя) складається з п'яти шарів: два згорткових шари з використанням максимальної пулінгової операції та три повнозв'язкові шари. Перший і другий згорткові шари містять d1 і d2 фільтрів відповідно де d1 / d2 ≃ 6 / 16. Графік залежності тестової помилки, позначеної як ϵ, від d1 на логарифмічній шкалі, що вказує на степеневу залежність з показником ступеня ρ∼0.4. Функція активації нейронів – ReLU.

Подібне явище степеневого закону також спостерігається для узагальненої архітектури VGG-16. Однак це призводить до збільшення кількості операцій, необхідних для досягнення заданого рівня помилки в порівнянні з LeNet.

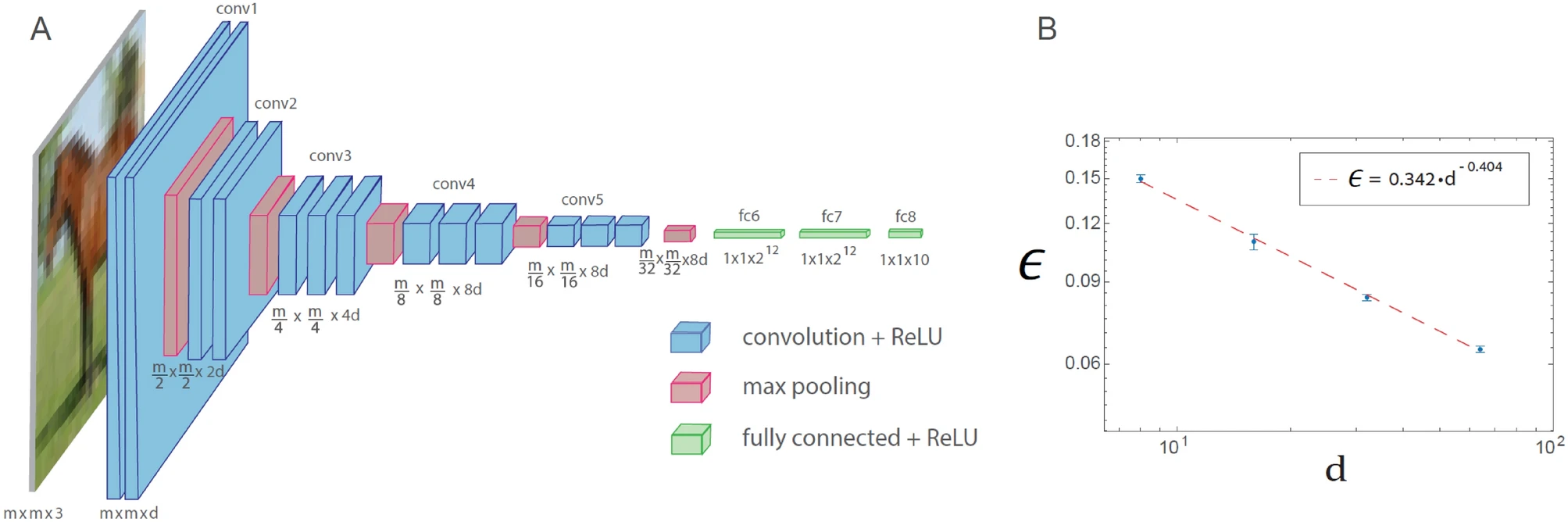
Навчання в узагальненій архітектурі VGG-16 наведено на рисунку нижче. Узагальнена архітектура VGG-16 складається з 16 шарів, де кількість фільтрів у n-му наборі згорток дорівнює d х 2n − 1 (n ≤ 4), а квадратний корінь від розміру фільтра дорівнює m х 2 − (n − 1) (n ≤ 5), де m x m x 3 – розмір кожного входу (d = 64 в оригінальній архітектурі VGG-16). Графік залежності тестової помилки, позначеної як ϵ, від d на логарифмічній шкалі для бази даних CIFAR-10 (m = 32), що вказує на степеневу залежність із показником ступеня ρ∼0.4. Функція активації нейронів – ReLU.

Феномен степеневого закону охоплює різні узагальнені архітектури LeNet та VGG-16, що вказує на його універсальну поведінку та свідчить про кількісну ієрархічну складність у машинному навчанні. Крім того, виявлено, що закон збереження для згорткових шарів, що дорівнює квадратному кореню від їх розміру, помноженому на їхню глибину, асимптотично мінімізує помилки. Показаний у цьому дослідженні ефективний підхід до поверхневого навчання потребує подальшого кількісного вивчення з використанням різних баз даних та архітектур, а також його прискореної реалізації за допомогою майбутніх спеціалізованих апаратних розробок.