RAG and Fine-Tuning are two methods to enhance Large Language Models like ChatGPT and Gemini, enabling access to external knowledge sources for up-to-date information retrieval without retraining. RAG improves input by retrieving external data, while Fine-Tuning adapts the model to specific requirements, revolutionizing LLM capabilities for various applications.
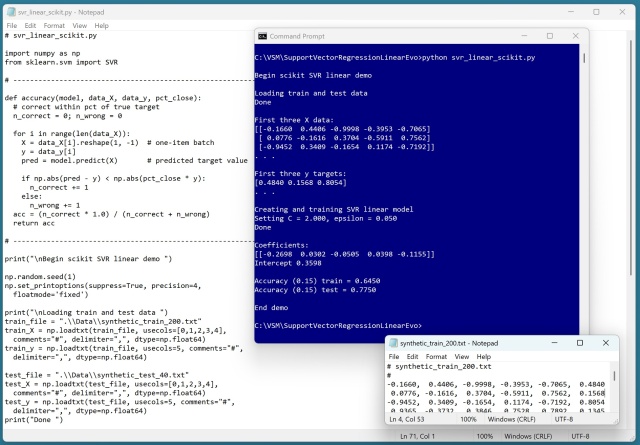
Support Vector Regression (SVR) with a linear kernel penalizes outliers more than close data points, controlled by C and epsilon parameters. SVR, while complex, yields similar results to plain linear regression, making it less practical for linear data.
Transitioning from Data Analyst to Data Scientist can be a smart career move. Marina from Amazon provides tips on skills, resources, and strategies for success.
FloTorch compared Amazon Nova models with OpenAI’s GPT-4o, finding Amazon Nova Pro faster and more cost-effective. Amazon Nova Micro and Amazon Nova Lite also outperformed GPT-4o-mini in accuracy and affordability.
Wall Street Journal's heatmaps show vaccines' impact on diseases in the US. Matplotlib's pcolormesh() recreates measles heatmap, showcasing data storytelling power.
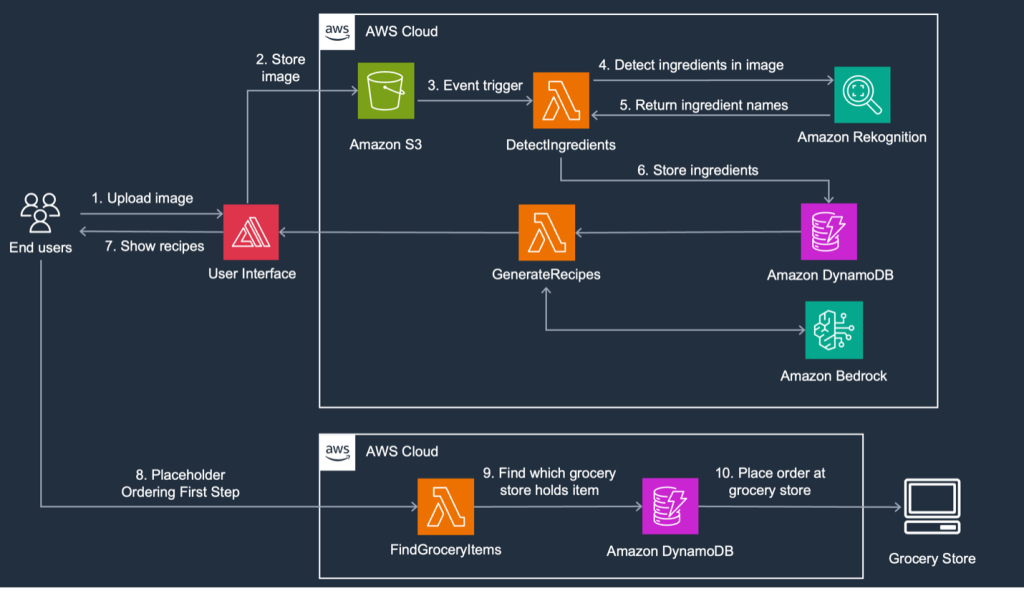
FoodSavr, a solution using generative AI on AWS, recommends recipes based on fridge contents and expiring items in local stores, reducing food waste and saving money. By utilizing Amazon Rekognition and Amazon Bedrock, users can upload fridge images to receive personalized recipes and nearby grocery store suggestions.
Techno-optimism resurges as billionaires envision a golden age through technology. San Francisco AI scenesters advocate for maximum acceleration of technological advancement in a viral manifesto.
Enthusiasts experiment with AI chatbot to recreate classic arcade games, with mixed results. Microsoft, Google, and xAI's Grok chatbot enable creation of virtual worlds and old arcade game clones, like a Pac-Man replica.
AI struggles to differentiate between similar dog breeds due to entangled features. PawMatchAI uses a unique Morphological Feature Extractor to mimic how human experts recognize breeds, focusing on structured traits.
Octus transforms credit analysis with AI-driven CreditAI chatbot, offering instant insights on thousands of companies. Octus migrated CreditAI to Amazon Bedrock, enhancing performance and scalability while maintaining zero downtime.
Researchers are tackling spurious regression in time series analysis, a critical issue often overlooked, with real-world implications. Understanding this concept is vital for economists, data scientists, and analysts to avoid misleading conclusions in their models.
Data team structure is crucial for leveraging Data and AI effectively. Centralized teams can become bottlenecks without proper domain expertise integration.
GPT-3 sparked interest in Large Language Models (LLMs) like ChatGPT. Learn how LLMs process text through tokenization and neural networks.
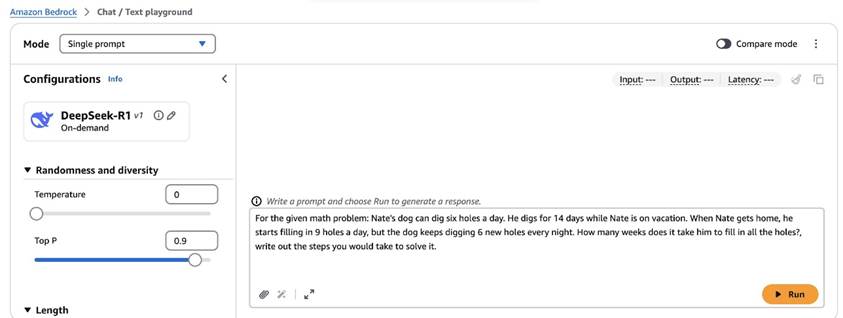
DeepSeek-R1 models on Amazon Bedrock Marketplace show impressive math benchmark performance. Optimize thinking models with prompt optimization on Amazon Bedrock for more succinct thinking traces.
LettuceDetect, a lightweight hallucination detector for RAG pipelines, surpasses prior models, offering efficiency and open-source accessibility. Large Language Models face hallucination challenges, but LettuceDetect helps spot and address inaccuracies, enhancing reliability in critical domains.