Is deep learning a necessary component of artificial intelligence?

In the world of artificial intelligence, the role of deep learning is becoming central. Artificial intelligence paradigms have traditionally taken inspiration from the functioning of the human brain, but it appears that deep learning has surpassed the learning capabilities of the human brain in some aspects. Deep learning has undoubtedly made impressive strides, but it has its drawbacks, including high computational complexity and the need for large amounts of data.

In light of the above concerns, scientists from Bar-Ilan University in Israel are raising an important question: should artificial intelligence incorporate deep learning? They presented their new paper, published in the journal Scientific Reports, which continues their previous research on the advantage of tree-like architectures over convolutional networks. The main goal of the new study was to find out whether complex classification tasks can be effectively trained using shallower neural networks based on brain-inspired principles, while reducing the computational load. In this article, we will outline key findings that could reshape the artificial intelligence industry.

So, as we already know, successfully solving complex classification tasks requires training deep neural networks, consisting of dozens or even hundreds of convolutional and fully connected hidden layers. This is quite different from how the human brain functions. In deep learning, the first convolutional layer detects localized patterns in the input data, and subsequent layers identify larger-scale patterns until a reliable class characterization of the input data is achieved.

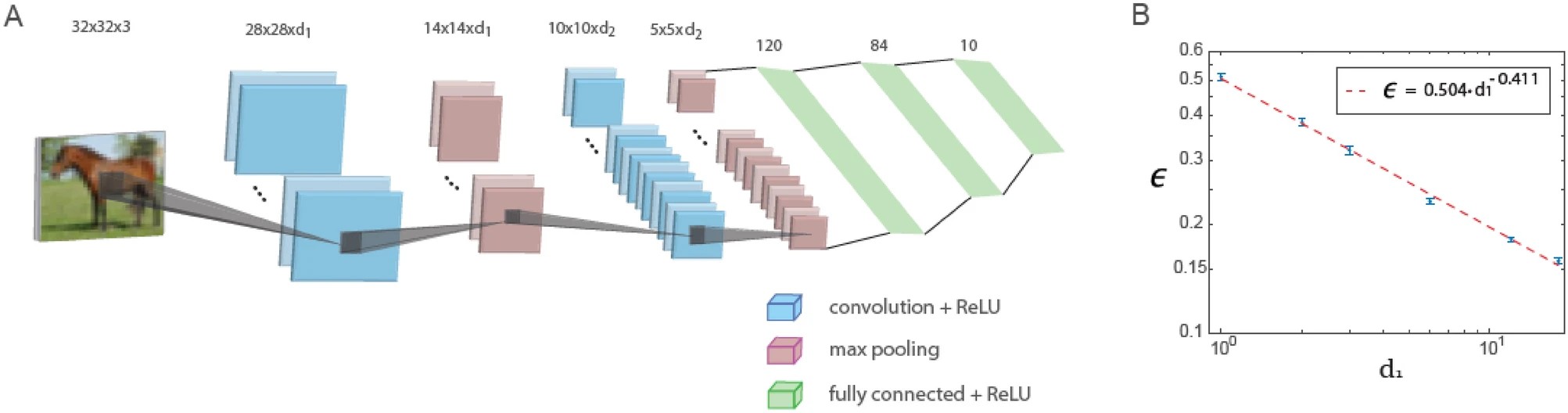
This study shows that when using a fixed depth ratio of the first and second convolutional layers, errors in a small LeNet architecture consisting of only five layers decrease with the number of filters in the first convolutional layer according to a power law. Extrapolation of this power law suggests that the generalized LeNet architecture is capable of achieving low error values similar to those obtained with deep neural networks based on the CIFAR-10 data.

The figure below shows training in a generalized LeNet architecture. The generalized LeNet architecture for the CIFAR-10 database (input size 32 x 32 x 3 pixels) consists of five layers: two convolutional layers using maximum pooling and three fully connected layers. The first and second convolutional layers contain d1 and d2 filters, respectively, where d1 / d2 ≃ 6 / 16. The plot of the test error, denoted as ϵ, versus d1 on a logarithmic scale, indicating a power-law dependence with an exponent ρ∼0.41. Neuron activation function is ReLU.

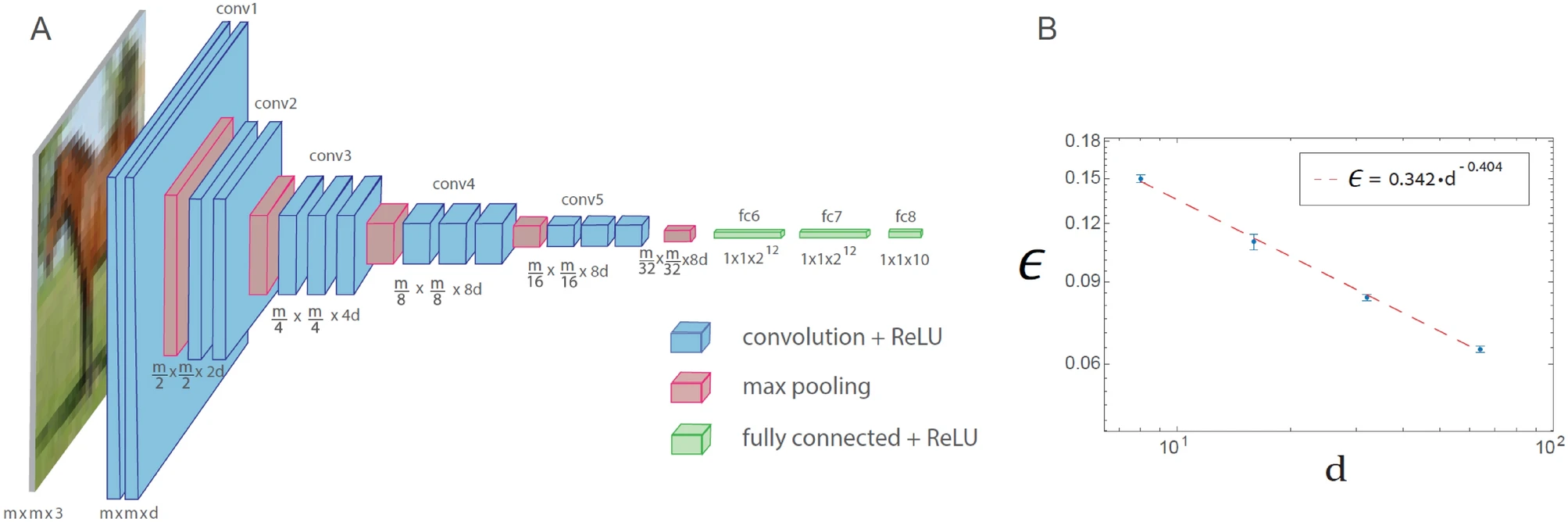
A similar power law phenomenon is also observed for the generalized VGG-16 architecture. However, this leads to an increase in the number of operations required to achieve a given error rate compared to LeNet.

Training in the generalized VGG-16 architecture is demonstrated in the figure below. The generalized VGG-16 architecture consisting of 16 layers, where the number of filters in the nth set of convolutions is d x 2n − 1 (n ≤ 4), and the square root of the filter size is m x 2 − (n − 1) (n ≤ 5), where m x m x 3 is the size of each input (d = 64 in the original VGG-16 architecture). Plot of the test error, denoted as ϵ, versus d on a logarithmic scale for the CIFAR-10 database (m = 32), indicating a power-law dependence with an exponent ρ∼0.4. Neuron activation function is ReLU.

The power law phenomenon covers various generalized LeNet and VGG-16 architectures, indicating its universal behavior and suggesting a quantitative hierarchical complexity in machine learning. In addition, the conservation law for convolutional layers equal to the square root of their size multiplied by their depth is found to asymptotically minimize errors. The effective approach to surface learning demonstrated in this study requires further quantitative study using different databases and architectures, as well as its accelerated implementation with future specialized hardware designs.